Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 05. 2020 18:10 — Editoval Zvedavec 4 (17. 05. 2020 01:57)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Hyperbolicky prubeh v STR
Kdysi jsem se docet, ze v STR maji nektere zmeny prubeh hyperboly. Nechtel jsem se ze zacatku zdrzovat badanim o cem to je.
Ale v prubehu jsem treba narazil na poznamku, mohlo to byt na wiki, ale nemuzu to tam ted najit, ze protoze jeden z tech badatelu do STR (nejspis to byl Lorentz) zjistil, ze jeden ze vzorecku STR pripomina rovnici prave hyperboly, dosel tim k zaveru, ze tomu tak nejspis bude.
Mam takovy dojem, ze to mohl byt prave vzorec pro interval casoprostoru  anebo
anebo 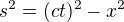 , ktery tedy vypada dost podobne jako zakladni rovnice h., co maji na wiki, tedy
, ktery tedy vypada dost podobne jako zakladni rovnice h., co maji na wiki, tedy 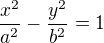 .
.
Pro intuitivni pochopeni STR asi potreba jit moc do detajlu nebude, ale je napriklad nejake vysvetleni, proc by tomu tak melo byt? Nikde jsem totiz na zadnou zminku o tom nenarazil.
Je mi celkem jasne, ze by to spis byl nejaky objev nebo teorie nebo i mereni nejakeho jineho fyzikalniho jevu, ktery by pak pomoci analogie pripisovali taky STR, jako se to deje pro nektere jine predpoklady o ni, protoze moc overeni o tom, jak pracuje v praxi jasne neexistuje.
Offline
#3 16. 05. 2020 20:47 — Editoval Zvedavec 4 (17. 05. 2020 02:04)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Hyperbolicky prubeh v STR
↑ edison:
Edisone, diky za nej.
Dival jsem se tam, hned jak's ho poslal. To jsem sem zrovna napsal ten priklad s  , na ktery jsem doufal dostat nejakou odpoved.
, na ktery jsem doufal dostat nejakou odpoved.
Ale tam nebyla a neodpovedel na nej nikdo ani po tom, co jsem sem poslal na nej link, a to bylo nakonec dobre.
I kdyz me to dalo zabrat, musel jsem ho nakonec rozlustit sam, coz bylo pro mne plus, ze jsem tomu problemu a pocetnim vzorcum STR s nim spojenym dobre porozumnel a rozlousknul zaroven i jejich zdanive neproniknutelna tajemstvi kvuli jejich az nekdy pro nematematika primo zvracenym anebo alespon az jakoby naruby prevracenym formam.
Ted jsem se do tech zizal taky podival, ale nenalezl. Na wiki jsou vysvetleni dobra, ale nekdy zavadejici. Ale mam na ty Zizaly link a tudiz mi jsou k mani, kdybych je potreboval.
Jenze abych to vsechno nemusel procitat a lamat si s tim pak hlavu, coz uz jsem udelal dost abych dosel az sem, shledavam mnohem rozumnejsi se obratit na toto forum, jako na ucitele, kde tem vecem uz rozumite. A navic urcite ruzne otazky radi odpovidate, prrotoze k tomu tady to forum je. A me otazky jsou z toho vseho, co jsem uz precet. A leccemu jsem skrze odpovedi na tomto foru porozumnel lip.
Otazka tohoto vlakna je nejspis moje posledni ohledne STR, protoze jsem uz jinak to ostatni vycerpal. A odpoved by jasne byla prospesna i ostatnim, coby si ji mohli precist.
Offline
#4 16. 05. 2020 21:04 — Editoval edison (16. 05. 2020 21:08)
Re: Hyperbolicky prubeh v STR
Problém celé sekce "Zajímavé a náročně..." je, že je úplně dole. Takže třeba já si většinou nevšimnu, že tam něco přibylo a když už tam pak je 10 obrazovek textu bez diakritiky, tak jsem línej to číst:-) To byl přesně případ těch 4 µs.
Já jsem v těhle věcech praktik. Hledám spíš jak vztahy s co nejmenším úsilím používat. Takže na jednu stranu takové věci, jako že z něčeho asi vyleze hyperbola na první pohled vidím, ale dál to nezkoumám, pokud to nevede třeba k usnadnění odhadu výsledku.
Offline
#5 17. 05. 2020 02:10 — Editoval Zvedavec 4 (17. 05. 2020 02:13)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Hyperbolicky prubeh v STR
Edisone, mrzi me to, ale bohuzel v pocitaci zadnou diakritiku, at uz pro Cestinu nebo i jinou, nemam. Mozna i proto, ze ho mam 10 let.
Protoze ja se snazim pochopit STR intuitivne tak me nezbyva, nez ty jeji vzorce rozebirat s pomoci sve rychle mizejici znalosti zakladni matematiky, jinak me nic nerikaji. A zda se jasne, ze hlavne Einstein a mozna i dalsi museli postupovat presne naopak. Nejdriv to museli vymyslet intuitivne a pak to dat do vzorcu. Nejake vzorce uz jiste existovaly, ale ne ty pro STR.
Takze na co jsem do ted intuitivne prisel, v podstate ty hlavni body STR jako dilatace, kontrakce, relativita soucasnosti, fazovy rozdil, interval casoprostoru atd., me staci. Ale to, ze prubehy nekterych velicin STR se meni po hyperbole ji delaji jeste zajimavejsi. Bylo by dobre to trochu rozvest.
Videl jsem taky na jedne ze stranek diagram nebo spis jenom nacrt, ze ktereho se dalo vycist, ze snad s primocarym narustem rychlosti se rychlost chodu casu tech rozlicnych soustav meni prave po te hyperbole.
To nejspis odpovida game, kde jak si vzpominam, nevim uz jak to spravne rict, ale snad ze funkce prevracene hodnoty da prave tu hyperbolu anebo, ze hyperbola je funkci prevracene hodnoty? Jenze tohle spolu s tim vzoreckem pro gamu ten jev uz jenom popisuji. Ale mozna je nejaka domenka, proc se to deje.
Offline
#6 17. 05. 2020 10:03
Re: Hyperbolicky prubeh v STR
Ano, nejjednodušší hyperboly jsou k/x. Složitější varianty nastávají, když mají bejt pootočené jinak.
Gama sice okolo bodu v=c vypadá jako hyperboly, ale nepokračuje plynule až do v= mínus nekonečno. O hyperbolu se tedy nejedná.
Ovšem OS, na kterém běží browser a nejde nainstalovat diakritika, ... to je exotika:-) To potom máš zmršený všechno co je normálně česky. Myslím, že by stačilo někde v nastavení přepnout lokalizaci na českou. Potom si to samo stáhne, nebo tě požádá o instalační CD (to by udělaly Windows z minulýho století).
Offline
#7 17. 05. 2020 11:32
Re: Hyperbolicky prubeh v STR
Áno, rovnice  je rovnicí hyperboly. Dokonce rovnoosé hyperboly (pokud máme správná měřítka).
je rovnicí hyperboly. Dokonce rovnoosé hyperboly (pokud máme správná měřítka).
A protože to je vlastně úplný základ STR, vyskytuje se to v ní v nějaké formě vlastně všude. Tak jako při otáčení souřadné soustavy se nám zachovává velikost vektoru - tedy 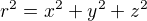 , a body při rotaci opisují pohyb po kružnici, stejně tak se při Lorentzově transformaci zachovává velikost čtyřvektroru, tedy
, a body při rotaci opisují pohyb po kružnici, stejně tak se při Lorentzově transformaci zachovává velikost čtyřvektroru, tedy 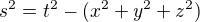 a "body časoprostoru" tedy události se tak pohybují po hyperbole.
a "body časoprostoru" tedy události se tak pohybují po hyperbole.
Věci jsou natolik podobné, že se Lorentzova transformace také někdy nazývá jako rotace, ale mě se to moc nelíbí, a taky jsem narazil na pojem "zobecněná hyperbolická rotace", který mi přijde poněkud výstižnější.
Offline
#8 17. 05. 2020 17:27 — Editoval Zvedavec 4 (17. 05. 2020 17:39)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Hyperbolicky prubeh v STR
↑ edison:
V podstatě z intuitivního hlediska jde jenom o ten nejprazákladnější princip a tedy všeobecnosti a ne nějaký specifika. A tedy ten základní tvar tý křivky je nejspíš to, bych předpokládal, co opisují ty zmíněný změny. Tedy tu 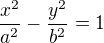 .
.
Ještě tedy zajímavější může být, jestli by ty změny měly dokonce průběhy různých konkrétních hyperbol, podle určitých podmínek, ale to se nachází mimo zájem obyčejný intuice.
Já jsem zas línej v hledání věcí o počítači v jeho vnitřnostech, jenom ho beru co výhodný náčiní, ale sám o sobě coby předmět "výzkumu" mě nijak nevzrušuje anebo spíš přímo votravuje, protože mě připadá, že tím plejtvám svůj drahocenej čas anebo i přímo sám život, a proto jsem tohle zanedbal a až na Tebe mě na to nikdo nepoukazoval.
A český texty, at' už tady na fo'ru nebo jinde, se vždycky s tou diakritikou ukazovaly.
Offline
#9 17. 05. 2020 17:59 — Editoval Zvedavec 4 (17. 05. 2020 18:02)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Hyperbolicky prubeh v STR
↑ MichalAld:
Tohle je určitě zajímavější i z hlediska obyčejné intuice.
Co by bylo tou jedničkou ve vzorci pro ten interval. Bylo by to 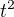 anebo to
anebo to 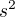 ?
?
Intuitivně bych se dohadoval, žeby snad ta 1 znamenala to, že se ta vlastní křivka nedotkne nikdy toho tzv. asymptotu a tedy byla nějak srovnatelná s tím, že se rychlost pohybu prostorem rychlostí  k rychlosti
k rychlosti  může jen do nekonečna přibližovat, ale nikdy ji nedosáhnout a měla by tím tedy snad zastupovat to
může jen do nekonečna přibližovat, ale nikdy ji nedosáhnout a měla by tím tedy snad zastupovat to 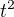 ?
?
Offline
#10 17. 05. 2020 21:42
Re: Hyperbolicky prubeh v STR
↑ Zvedavec 4:
Jednička by byla samozřejmě to 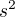 , ale nemusí to být nutně jednička, může to být jakékoliv číslo.
, ale nemusí to být nutně jednička, může to být jakékoliv číslo.
Nejjednodušší je podle mě k tomu přistupovat jako ke klasické rotaci.
Takže když budeme mít 2D prostor (rovinu s osami x, y), někde v té rovině si zvolíme bod, a pak bychom postupně (po malých krůčcích) prováděli transformaci rotace (otáčení) souřadné soustavy, bude náš bod opisovat kružnici o poloměru 
Ve skutečnosti stojí bod "na stejném místě" a otáčí se ty souřadné soustavy...
No a v STR je to (skoro) úplně stejné. Vezmeme si 1D1T časoprostor (opět je to rovina, jen s osami x, t), zvolíme si nějakou událost a zase provádíme transformaci "rotace" (Lorentzovu transformaci) soustavy ... a náš bod tak opisuje onu hyperbolu o "poloměru" 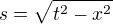
Je ovšem třeba vzít v úvahu jisté odlišnosti ... díky tomu zápornému znaménku může být "poloměr" i nulový, případně může být výraz pod odmocninou záporný ... a pak musíme x a t prohodit.
Offline
#11 19. 05. 2020 18:29 — Editoval Zvedavec 4 (19. 05. 2020 22:45)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Hyperbolicky prubeh v STR
Takže tohle je sice hodně zajímavé, ale je to už mimo dosah mých aspirací do intuitivního zvládnutí STR.
A protože toho všeho je tolik nemyslel bych si, že i na tohle všechno přišli v rámci STR, ale že to už spíš muselo být známo před tím?
Těmhle různým diagramům jsem moc pozornosti nevěnoval, i když jsem je probádal, když jsem si myslel, že by mě mohly pomoct s intuicí, na co jsou kolikrát hodně dobrý.
S rotacema jsem čas neztrácel a ani bych nevěděl, co si o nich myslet. Vidím ale, že můžou být hodně užitečný pro víc detajlní rozbor.
Dávám sem svůj výpočet toho, jak bych si myslel, že by se to asi počítalo. 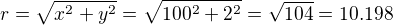
Kdyz tedy potocim ty osy tak, ze se ten bod octne na x, tedy 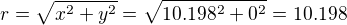 a kdybych je natocil tak, ze se ten bod nachazi presne uprostred, tak pak snad
a kdybych je natocil tak, ze se ten bod nachazi presne uprostred, tak pak snad 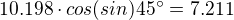 a tedy x=7.211 a y=7.211 a tedy
a tedy x=7.211 a y=7.211 a tedy 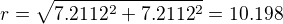 .
.
To je úžasný, to jsem vskutku netušil !
Pro ten interval časoprostoru by to pak asi muselo být takhle:
s= 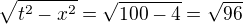 =9.797 958 971
=9.797 958 971
Potom tedy po natoceni tak, zeby pri x'=9.797 958 971 a t'=0 by s'=9.797 958 971.
Pri 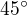 by vychazelo s=
by vychazelo s=  =0
=0
Tohle by snad znamenalo, že by se ten bod objevil na jednom z těch jejích tzv asymtotů? Tedy v nekonečnu?
Pri  by pak vychazelo:
by pak vychazelo:
s=  =6.928 203 23
=6.928 203 23
Pri 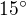 by to bylo s=
by to bylo s=  =
=  =
=  =
=  =9.118 028 228
=9.118 028 228
Vidím, že výsledek pro počítání toho kruhu je dobře.
Ale jak by se mohlo ověřit z těch vyšlých čísel, že výpočet rotace pro ten interval časoprostoru je dobře, anebo že by i vůbec dával nějaký smysl, a tedy skutečně dává hyperbolu, mi není jasné.
Takže ve skutečnosti se snad pohybuje ten bod v těch souřadnicích než ty souřadnice samotné anebo je to spíš pohyb relativní obou vůči sobě navzájem.
Ale když se bude něco rotovat, tedy to už bude pohyb v kruhu, nezapadá to už spíš do OTR, jak jsem se dočet?
Offline
#12 19. 05. 2020 19:29
Re: Hyperbolicky prubeh v STR
Zvedavec 4 napsal(a):
Takže tohle je sice hodně zajímavé, ale je to už mimo dosah mých aspirací do intuitivního zvládnutí STR.
Škoda že tvá intuice nezvládá počítání s písmeny a všude musíš cpát ta čísla.
Zvedavec 4 napsal(a):
A protože toho všeho je tolik nemyslel bych si, že i na tohle všechno přišli v rámci STR, ale že to už spíš muselo být známo před tím?
Nic z toho před tím známé nebylo, všechno bylo objeveno až potom. Ale není to vlastně žádná nová fyzika, je to jen hlubší pohled na to, jak chápat Lorentzovu transformaci.
Offline
#13 19. 05. 2020 19:31 — Editoval MichalAld (19. 05. 2020 19:33)
Re: Hyperbolicky prubeh v STR
Zvedavec 4 napsal(a):
Pro ten interval časoprostoru by to pak asi muselo být takhle:
= 9.797 958 971
Potom tedy po natoceni tak, zeby pri x'=9.797 958 971 a t'=0 by s'=9.797 958 971.
Pri 45* by vychazelo= 0
Tohle by snad znamenalo, že by se ten bod objevil na jednom z těch jejích tzv asymtotů? Tedy v nekonečnu?
Jenže pro zobecněné hyperbolické rotace musíš také používat hyperbolické funkce, tedy sinh, cosh. A do těch se nedosazuje ve stupních...
Navíc tvá představa, že  není tak úplně správná.
není tak úplně správná.
Offline
#14 19. 05. 2020 23:31 — Editoval Zvedavec 4 (20. 05. 2020 00:43)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Hyperbolicky prubeh v STR
Na to abych, coby nematematik, vytušil, co si představit pod  si pomocí čísel rozepisovat nemusím, na to opravdu vystačí intuice, ale na
si pomocí čísel rozepisovat nemusím, na to opravdu vystačí intuice, ale na  už si ty čísla dosadit budu muset.
už si ty čísla dosadit budu muset.
Ta rotace v te tzv. Euklidově rovině(?), kde tedy vychází kruh, je vlastně, bych řekl, pouhé skládání do sebe základní trigonometrie. Ale říkáš, že to bylo vymyšleno až teprve v rámci STR. Nejspíš tedy musíš mít na mysli tu rotaci druhou?
Jo, v jednom místě jsem to špatně napsal z důvodu, že jednak nejenom bylo samo o sobě hodně náročný s těma číslama pracovat, a navíc pod nátlakem možnosti, že mě celý rozpracovaný text z toho pracovního pole zmizí (jako se mi to stalo minule), ale navíc jsem zjistil, že se tam celý ten postup nevešel a musel jsem to celý narychlo (ze stejné obavy) upravovat. Nakonec jsem to napsal špatně, ale vyšlo mi to dobře!
Nechtěl jsem sem takovou celkem malichernou otázku, proč by měly sinhy a kosinhy, na rozdíl od sínů a kosínů, vycházet v číslech tak astronomických už od 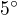 dávat. Takže když nevychází ve stupních v čem tedy? Ale astronomický zůstávají. Protože už
dávat. Takže když nevychází ve stupních v čem tedy? Ale astronomický zůstávají. Protože už  pak při odmocnění pořád dá 4,179,370,231!
pak při odmocnění pořád dá 4,179,370,231!
Ale proč se pak  ? Tohle přece je P.věta. Takže pak by ta čísla, co mě vyšla podle pouhé trigonometrie/P.věty měla být správná.
? Tohle přece je P.věta. Takže pak by ta čísla, co mě vyšla podle pouhé trigonometrie/P.věty měla být správná.
Offline
#15 20. 05. 2020 20:33 — Editoval Zvedavec 4 (24. 05. 2020 16:27)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Hyperbolicky prubeh v STR
MichalAld napsal(a):
↑ Zvedavec 4:
Nejjednodušší je podle mě k tomu přistupovat jako ke klasické rotaci.
........
No a v STR je to (skoro) úplně stejné. Vezmeme si 1D1T časoprostor (opět je to rovina, jen s osami x, t), zvolíme si nějakou událost a zase provádíme transformaci "rotace" (Lorentzovu transformaci) soustavy ... a náš bod tak opisuje onu hyperbolu o "poloměru"
Problemém tady jasně je, že při  by
by  muselo být
muselo být  , protože nemůže být žádný pohyb časoprostorem bez plynutí času.
, protože nemůže být žádný pohyb časoprostorem bez plynutí času.
Když  a
a 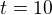 , jak jsem si zadal podle toho, jak mi bylo navrženo, které jsou sice srovnatelné pro výpočet P.věty, ale vůbec né pro výpočet toho intervalu, tak to nemůže vyjít. Taky protože tam hraje roli rychlost pohybu
, jak jsem si zadal podle toho, jak mi bylo navrženo, které jsou sice srovnatelné pro výpočet P.věty, ale vůbec né pro výpočet toho intervalu, tak to nemůže vyjít. Taky protože tam hraje roli rychlost pohybu  a hlavne se musí zahrnout konstanta
a hlavne se musí zahrnout konstanta  .
.
Moje zadané zkušební hodnoty byly tedy absolutně nesrovnatelné, jak je vidět. Aby to vůbec nějak s těma nesrovnatelnýma hodnotama vyšlo, musel jsem to počítat v počítači a tak to sem dávám, když už jsem se s tím počítal, k posouzení, ale jenom těžko se to sem vejde: . Potom
. Potom 

Zase tady vyniká to, že ten interval časoprostoru  znamená vzdálenost, o kterou se těleso "v pohybu" přemístí časem. V tomhle příkladě je to po tom, co uplyne
znamená vzdálenost, o kterou se těleso "v pohybu" přemístí časem. V tomhle příkladě je to po tom, co uplyne  v soustavě "v klidu". A jak STR tvrdí, čím je větsi rychlost tělesa "v pohybu", tím bude
v soustavě "v klidu". A jak STR tvrdí, čím je větsi rychlost tělesa "v pohybu", tím bude  menší.
menší. a tedy potom
a tedy potom  , tedy
, tedy  !
!
Tak, jak jsem si to zadal se zdálo srovnatelné, protože jsem měl na mysli P.větu. Ale jak vidět, rychlost  se do počtů s relativitou moc nehodí !
se do počtů s relativitou moc nehodí !
Jinak to, Michale, je dobré poukázání na vůbec existenci takovýchto rotací k počízání STR a dá to zvláštní pohled na to, jak to pracuje z pohledu geometrie.
Jaká by byla výhoda použít rotaci namísto přímého výpočtu mi není současně jasné. Takže jestli tu svou ukázku dokončíš tak snad uvidím, kde jsem udělal chybu.
Jde o to, že ta Lorenzova transformace je ukázka toho, jak STR pracuje z hlediska geometrie a dá se tedy říct, že by to byl ten intuitivní pohled.
Offline
#16 23. 05. 2020 20:52 — Editoval Zvedavec 4 (24. 05. 2020 16:25)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Hyperbolicky prubeh v STR
edison napsal(a):
Ovšem OS, na kterém běží browser a nejde nainstalovat diakritika, ... to je exotika:-) To potom máš zmršený všechno co je normálně česky. Myslím, že by stačilo někde v nastavení přepnout lokalizaci na českou. Potom si to samo stáhne, nebo tě požádá o instalační CD (to by udělaly Windows z minulýho století).
Zas taková exotika můj laptop není. Anichž bych se po tom nějak aktivně pídil, protože jsem vlastně ty diakritika nepotřeboval, říkal jsem si v duchu, že i kdyby nějaký takový program existoval, jak bych ho mohl využít, když moje klávesnice písmenka s háčkama a čárkama stejně nemá. Ted´ tedy vím jak, ale je to o to větší fuška je najít!
edison napsal(a):
Gama sice okolo bodu v=c vypadá jako hyperboly, ale nepokračuje plynule až do v= mínus nekonečno. O hyperbolu se tedy nejedná.
Protože  a interval časoprostoru jsou jenom trochy jiný koncept stejného principu, ale jinak početně v podstatě to samé, když tedy
a interval časoprostoru jsou jenom trochy jiný koncept stejného principu, ale jinak početně v podstatě to samé, když tedy  ten průběh nemá, jak by ho moh´ mít ten interval, by byla logická otázka. A potom tedy, v čem jiném by ta h. vězela?
ten průběh nemá, jak by ho moh´ mít ten interval, by byla logická otázka. A potom tedy, v čem jiném by ta h. vězela?
Offline
#17 24. 05. 2020 17:23 — Editoval Zvedavec 4 (24. 05. 2020 17:32)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Hyperbolicky prubeh v STR
Při pohledu na základní rovnici hyperboly 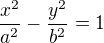 na wiki se zdá jasné, že ten její pravoúhlý trojúhelník o stranách a, b, c určuje sklon těch jejích asymptotů, a proto nejspíš když a=1, b=1, a=b, a tedy
na wiki se zdá jasné, že ten její pravoúhlý trojúhelník o stranách a, b, c určuje sklon těch jejích asymptotů, a proto nejspíš když a=1, b=1, a=b, a tedy 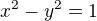 a potom tedy
a potom tedy 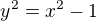 by měl být vzorec, se kterým by se počítalo, protože ty geometrické rozbory v STR, jak jsem se několikrát dočet, jsou většinou založený na kuželu s
by měl být vzorec, se kterým by se počítalo, protože ty geometrické rozbory v STR, jak jsem se několikrát dočet, jsou většinou založený na kuželu s  sklonem.
sklonem.
Potom tedy aby se dalo mluvit o hyperbole, bych si myslel, že tenhle tvar, a to hlavně včetně té  , se bude muset zachovat, protože to snad je právě ta
, se bude muset zachovat, protože to snad je právě ta  , co mu význam té h. dává, nebo né?
, co mu význam té h. dává, nebo né?
Protože ale ta  tady neznamená celek, ale opravdovou
tady neznamená celek, ale opravdovou  , nepřišel jsem zatím na to, co tam dosazovat aby se daly nějak "propojovat" výpočty těch dvou vzorců, tedy toho pro tu h. s tím pro ten interval tak aby to dávalo nějaký smysl!
, nepřišel jsem zatím na to, co tam dosazovat aby se daly nějak "propojovat" výpočty těch dvou vzorců, tedy toho pro tu h. s tím pro ten interval tak aby to dávalo nějaký smysl!
Offline
#18 25. 05. 2020 19:54
Re: Hyperbolicky prubeh v STR
edison napsal(a):
Gama sice okolo bodu v=c vypadá jako hyperboly, ale nepokračuje plynule až do v= mínus nekonečno. O hyperbolu se tedy nejedná.
Vztah pro  není rovnice hyperboly, ale převrácené kružnice.
není rovnice hyperboly, ale převrácené kružnice.

Hyperbolická závislost by musela být ve tvaru
Offline
#19 25. 05. 2020 23:41 — Editoval Zvedavec 4 (25. 05. 2020 23:50)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Hyperbolicky prubeh v STR
Na wiki se píše, co si ještě jenom matně pamatuju ze školy, že křivka, co představuje funkci f(x)=1/x, je hyperbola.
MichalAld napsal(a):
Vztah pro
není rovnice hyperboly, ale převrácené kružnice.
Znamenalo by tohle, alespoň nějak v principu, že aby vynikla hyperbola musely by se na osu  vynášet hodnoty, coby se zvětšovaly rovnoměrně, tedy by rostly tzv. přímočaře, tedy tzv. lineárně, a na osu
vynášet hodnoty, coby se zvětšovaly rovnoměrně, tedy by rostly tzv. přímočaře, tedy tzv. lineárně, a na osu  by se pak musely nanést jejich obrácené hodnoty?
by se pak musely nanést jejich obrácené hodnoty?
Ale protože  , coby výsledek rozdílu čtverců, tuhle podmínku, bych se jenom mohl domnívat, nensplńuje, nanesením na osu
, coby výsledek rozdílu čtverců, tuhle podmínku, bych se jenom mohl domnívat, nensplńuje, nanesením na osu  obrácených hodnot tohoto početního vztahu by proto hyperbola vzniknout nemohla, ale jenom ta tzv.převrácená kružnice?
obrácených hodnot tohoto početního vztahu by proto hyperbola vzniknout nemohla, ale jenom ta tzv.převrácená kružnice?
Offline
#20 26. 05. 2020 18:00 — Editoval MichalAld (26. 05. 2020 18:01)
Re: Hyperbolicky prubeh v STR
Zvedavec 4 napsal(a):
Na wiki se píše, co si ještě jenom matně pamatuju ze školy, že křivka, co představuje funkci f(x)=1/x, je hyperbola.
Je to hyperbola, ale otočená o 45°. Takovéto závislosti se říká nepřímá úměrnost.
Pokud mluvíme o hyperbolické závislosti nebo geometrii, máme na mysli funkci typu (všechny koeficienty předpokládáme kladné)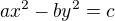
případně tedy 
Jinak samozřejmě úplně obecná rovnice kuželosečky je (zde už mohou být čísla i záporná)
To zahrnuje úplně všechny varianty, i všechna možná natočení. Takže i variantu  , která představuje zrovna hyperbolu.
, která představuje zrovna hyperbolu.
Ale ta hyperbola, co se "podobá kružnici" - tak to je ta, co jsem zmínil na začátku. Protože ta se od kružnice či elipsy liší jen znaménkem.
Offline