Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » pravidelný jehlan s vepsanou krychlí (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 03. 2010 15:05
pravidelný jehlan s vepsanou krychlí
Dobrý den, potřebuju poradit s tímhle příkladem:
Do pravidelného čtyřbokého jehlanu s podstavnou hranou délky a je vepsána krychle tak, že jedna její stěna leží v podstavě jehlanu
a zbylé čtyři vrcholy jsou středy bočních hran jehlanu.
Objem této krychle je?
- nějak si nedovedu představit, že stěna krychle leží v podstavě jehlanu a zárověň se dotýká bočních hran jehlanu v jejich polovině.
(nemám výsledek, příklad je z ukázky, kterou jsem stáhl z webu scio)
Offline
- (téma jako vyřešené označil(a) trife)
#2 16. 03. 2010 15:31 — Editoval Rumburak (16. 03. 2010 16:13)
Re: pravidelný jehlan s vepsanou krychlí
Snadno nahlédneme, že hrana vepsané krychle má velikost 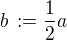 , což je zároveň polovina výšky
, což je zároveň polovina výšky  jehlanu.
jehlanu.
Takže 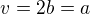 a stačí pak dosadit do známého vzorce.
a stačí pak dosadit do známého vzorce.
PS. Jak si krychli představit ? Označme A, B, C, D vrcholy podstavy jehlanu, V jeho hlavní vrchol, K, L, M, N po ředě středy hran
AV, BV, CV, DV . Body K, L, M, N jsou tedy těmi vrcholy krychle, které neleží v podstave ABCD jehlanu. Zbývající vrcholy P, Q, R, S
krychle získáme takto: z bodu K spustíme kolmici na podstavu jehlanu a její patu označíme P - obecně "dolní" vrcholy
krychle obdržíme jako kolmé průměty "horních" vrcholů K, L,M, N do podstavy jehlanu.
Tímto způsobem sestrojený šestistěn PQRSKLMN ovšem nebude v obecném případě krychlí, ale pouze pravidelným čtyřbokým hranolem
s podstavnou hranou
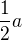 a výškou
a výškou 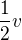 . Zadání úlohy však říká, že JE TO KRYCHLE, takže potom nutně
. Zadání úlohy však říká, že JE TO KRYCHLE, takže potom nutně  .
. Offline
#3 27. 05. 2020 12:29
- Bdbsjnsxj
- Zelenáč
- Příspěvky: 4
- Škola: Biskupské gymnaziun J. N. Neumanna ČB
- Pozice: Student
- Reputace: 0
Re: pravidelný jehlan s vepsanou krychlí
Dobrý den, potřebovala bych poradit s tímto příkladem.
Pravidelnému čtyřbokému jehlanu s výškou v a délkou podstavné hrany a je vepsána kachle tak, že vrcholy jedné její stěny leží na osách bočních stěn jehlanu. Určete délku hrany krychle.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » pravidelný jehlan s vepsanou krychlí (TOTO TÉMA JE VYŘEŠENÉ)
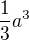 .
.