Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 05. 2009 18:17
- docasne123
- Příspěvky: 56
- Reputace: 0
Tečny ke kružnicím - polára
Ahoj,
chci se zeptat jestli je možné vyjádřit 4 společné tečny pro dvě kružnice (které nemají společné body dotyku) pomocí rovnice poláry. Mám na mysli že by se do rovnice poláry jedné kružnice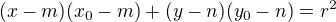
dosadilo za "x nula" a "y nula" vyjádřené "x" a "y" z 2. rovnice kružnice. S dovolením uvedu i příklad.

vzniká (?) =>![kopírovat do textarea $p : (x - 10)[(\sqrt{5}-y) - 10]+y(\sqrt{5}-x) = 45$](/mathtex/64/64d96cf42400ba1dc8e144bf24b023ea.gif)
Výsledek už mám spočítáný jiným způsobem, jen by mě zajímalo jestli by to teoreticky nešlo i tímto způsobem.
Děkuji
Offline
#2 09. 06. 2009 16:46 — Editoval musixx (09. 06. 2009 16:47)
Re: Tečny ke kružnicím - polára
To  ale neni primka. Rovnice polary
ale neni primka. Rovnice polary  potrebuje kruznici
potrebuje kruznici 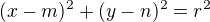 a bod
a bod ![kopírovat do textarea $[x_1,y_1]$](/mathtex/08/081bb760981fb136f88ed2b93585aa8b.gif) . Umim si predstavit, ze za bod
. Umim si predstavit, ze za bod ![kopírovat do textarea $[x_1,y_1]$](/mathtex/08/081bb760981fb136f88ed2b93585aa8b.gif) se vezme stred stejnolehlosti techto dvou kruznic (existuji dva, a to vlastne i v pripade kruznic o stejnem polomeru, uvazuji-li rozsirenou rovinu). Takovy stred se hleda snadno, staci uvazit spojnici stredu a deleni teto usecky v pomeru polomeru techto kruznic (a analogicky pro stred druhe stejnolehlosti). Pak timto stredem konstruovat polaru k jedne z kruznic a to, ze takto ziskana tecna k teto kruznici bude i tecnou ke druhe kruznici, je jasne.
se vezme stred stejnolehlosti techto dvou kruznic (existuji dva, a to vlastne i v pripade kruznic o stejnem polomeru, uvazuji-li rozsirenou rovinu). Takovy stred se hleda snadno, staci uvazit spojnici stredu a deleni teto usecky v pomeru polomeru techto kruznic (a analogicky pro stred druhe stejnolehlosti). Pak timto stredem konstruovat polaru k jedne z kruznic a to, ze takto ziskana tecna k teto kruznici bude i tecnou ke druhe kruznici, je jasne.
Offline
#3 09. 06. 2009 17:07
Re: Tečny ke kružnicím - polára
Zkusme se zamyslet nad tím, je-li vůbec možné chtít analogicky k poláře hledat nějakou křivku p, která protíná kružnici (kružnice) právě v bodech dotyku společných tečen.
Neuvažujme žádné degenerované případy.
S polárou k jedné kružnici je to snadné: je to přímka protínající tuto jedinou kružnici ve dvou bodech.
S polárou popisující společné tečny ke dvěma kružnicím je to jiné (uvažme třeba kružnice o různých poloměrech, neležící uvnitř sebe a neprotínající se, ať je situace jasná). Taková polára určitě nebude přímka - vždyť na jedné kružnici jsou 4 body dotyku a stejně tak na druhé. Průsečíky se kterou z těchto kružnic hledáme může být dáno tím, do které rovnice kružnice "dosazujeme". Jenže "dosazovat" body z druhé kružnice se mi nezdá: vždyť žádným bodem jedné kružnice nebudou procházet dvě společné tečny ke druhé kružnici.
Ještě nad tím popřemýšlím, ale stejně si myslím, že pokud se dobereme k nějakému výsledku, tak to bude maximálně teoreticky použitelné. Jako nejsnáze spočitatelné se ji staále jeví ty středy stejnolehlostí + poláry k jedné z kružnic.
Offline
