Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 14. 06. 2020 12:25 — Editoval Ferdish (14. 06. 2020 17:14)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Determinant
Vyzerá to na všeobecnú maticu 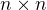 , kde nie je určené či
, kde nie je určené či  je párne alebo nepárne, všetky prvky na hlavnej diagonále majú hodnotu
je párne alebo nepárne, všetky prvky na hlavnej diagonále majú hodnotu  , všetky prvky "nad" hlavnou diagonálou majú hodnotu
, všetky prvky "nad" hlavnou diagonálou majú hodnotu  a prvky "pod" hlavnou diagonálou
a prvky "pod" hlavnou diagonálou 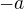 .
.
Ak uvedená konfigurácia platí ľubovoľné  , potom môžeš skúsiť odhadnúť nejaký rekurentný postup. Vyrieš determinanty takto zadaných matíc pre
, potom môžeš skúsiť odhadnúť nejaký rekurentný postup. Vyrieš determinanty takto zadaných matíc pre 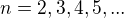 a porovnaj ich, či sa tam neobjavuje nejaká zjavná funkčná závislosť na
a porovnaj ich, či sa tam neobjavuje nejaká zjavná funkčná závislosť na  (nemusí byť zrovna jednoduchá).
(nemusí byť zrovna jednoduchá).
Ak by to nevychádzalo, potom skús využiť vlastnosť, že pri výpočte determinantu takto zadanej matice rozmeru  sa ti pri rozvoji podľa riadku určite objaví determinant tej istej matice rozmeru
sa ti pri rozvoji podľa riadku určite objaví determinant tej istej matice rozmeru  . Znova si to skús pre nejaké malé čísla. Myslím že už pre najnižšie možné
. Znova si to skús pre nejaké malé čísla. Myslím že už pre najnižšie možné 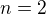 tam možno niečo vidieť.
tam možno niečo vidieť.
Offline
#3 14. 06. 2020 17:10 — Editoval vanok (14. 06. 2020 17:18)
Re: Determinant
Ahoj ↑ ivcam:,
Je viacej moznosti na riesenie tohto cvicenia.
Mozes to po uprave tvojej matice pouzit indukciu.
Alebo uvazuj maticu U, nxn ktorej cleny su 1 a dana sa oznaci M: potom matica M-tU ma zaujimavay determinant, ktory je polynom v t...
( pozri aj tu https://forum.matweb.cz/viewtopic.php?pid=248058 v # 12 som o podobnom pisal).
Pozdravujem ↑ Ferdish:,
Co to je pojem nizkeho cisla? Nikdy som take nepocul.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 14. 06. 2020 17:19
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Determinant
↑ vanok:
V niektorých iných oblastiach ako matematika ide o celkom zaužívaný termín. Napr. fotografovanie a pojem vysokého alebo nízkeho clonového čísla :-)
Ale chápem, že v kontexte matematiky toto označenie vyznieva neohrabane. Opravené.
Offline
#5 14. 06. 2020 19:11
Re: Determinant
↑ ivcam:
Ahoj, vem posledni radek a pricti ho k prvnimu. Naopak, od druheho az (n-1)-ho posledni radek odecti.
Pak udelej rozvoj determinantu podle prvniho radku a nasledne podle prvniho sloupce.
Ziskas rekurentni vztah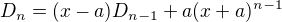
Diferencni rovnici vyres, nebo dokaz matematickou indukci, ze![kopírovat do textarea $D_n = \frac{1}{2}\Bigr[(x+a)^n+(x-a)^n\Bigr]$](/mathtex/6d/6d367ca047923f4cc85c74f6a652fa8c.gif)
Offline
#6 14. 06. 2020 22:48
Re: Determinant
Ahoj ↑ ivcam:,
(Servus ↑ laszky:, ano, no pridam dalsie indikacie na tu druhu metodu).
Tu ↑ vanok:, ak konstatujes, ze 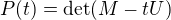 je polynome najviac prveho stupna, a tak
je polynome najviac prveho stupna, a tak 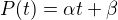 .
.
Potom lahko urcis aj tvoj determinant.
Dokazes to?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 14. 06. 2020 23:37 — Editoval vanok (14. 06. 2020 23:38)
Re: Determinant
Ahoj ↑ ivcam:,
Napisem ti ako mozes prist k rieseniu vdaka tej druhej metode .
Co sa tyka stupna polynomu P staci opocitas prvy stlpec od vsetkych inych a ho a potom ho rozvinies podla neho.
( nemusis ho ani pocitat, staci vidiet, ako ten determinant vyzera).
Preto staci mat dve hodnoty toho 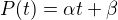 ( P(a) a P(-a) velmi lahko najdes, ide o o determinant trojuholnikovej matice.... ktory je sucin prvkov diagonaly). A nakoniec P(0) je hladany determinant.
( P(a) a P(-a) velmi lahko najdes, ide o o determinant trojuholnikovej matice.... ktory je sucin prvkov diagonaly). A nakoniec P(0) je hladany determinant.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

