Matematické Fórum

Vladimir9O · 16. 06. 2020 18:48

Když v= dt/ds (někdy se d nahradí řeckým písmenem delta) nám bylo řečeno jako "změna v čase" (kdysi dávno, na hodinách fyziky).

To jsou jako derivace, nebo se to dá nějak obejít?

edison · 16. 06. 2020 19:11

ano, d je při derivaci. V podstatě se tím říká, že delta řídící veličiny je limitně blízké 0. Takže "obejití" může spočívat v tom, že delta s zvolíme zanedbatelně malé.

vlado_bb · 16. 06. 2020 19:13

↑ Vladimir9O:Pri obvyklom znaceni je 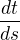$\frac{dt}{ds}$ derivaciou casu podla drahy :)

pietro · 16. 06. 2020 19:15

v=ds/dt

MichalAld · 16. 06. 2020 19:22

Obejít se to nedá...a ano, fyzikové pojem derivace nepoužívají příliš rádi, když jde o interpretaci fyzikálních veličin.

Není ovšem těžké si selským rozumem představit, co to vlastně je, protože přibližně je rychlost to co jsi zmínil, totiž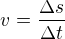

$v = \frac{\Delta s}{\Delta t}$

a ty "delty" představují nějaké malé elementy dráhy a času. Čím budou menší, tím určíme tu okamžitou rychlost přesněji. Prostě potřebujeme, aby se ta rychlost v rámci těch elementů (moc) neměnila. Samozřejmě - je li rychlost konstantní, potom na velikosti těch elementů nezáleží.

Matematická derivace je prostě tahle úvaha dotažená k dokonalosti ... že ty elementy zmenšujeme až jsou nekonečně malé. Sice to vypadá hrozně bláznivě, ale ve skutečnosti je to celkem elegantní způsob, jak tu rychlost určit. Jistě, stojí za tím kupa matematické teorie, když to chceme mít opravdu bez vad, ale tu většinou nemusíme znát.

Pokud by se třeba poloha měnila v čase dle vzahu 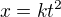$x = kt^2$ , tedy s druhou mocninou, můžeme zkusit spočítat tu rychlost.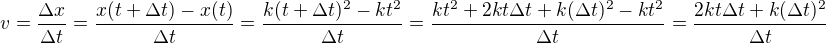

$v = \frac{\Delta x}{\Delta t} = \frac{x(t+\Delta t) - x(t)}{\Delta t} = \frac{k(t+\Delta t)^2 - kt^2}{\Delta t}= \frac{kt^2 + 2kt \Delta t + k (\Delta t)^2 - kt^2}{\Delta t} = \frac{2kt \Delta t + k (\Delta t)^2}{\Delta t}$

No a teď bychom potřebovali to spočítat když to $\Delta T$ bude velmi malé. Víme, že když by bylo rovnou nulové, tak to spočítat nedokážeme, protože bychom dostali 0/0 a to spočítat neumíme. Ale pro každé jiné $\Delta T$ můžeme zlomek normálně zkrátit, takže dostaneme

$v = 2kt + k \Delta T$

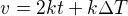
No a teď už je zřejmé, že pro velmi malé 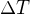$\Delta T$ bude velmi malý i ten druhý člen, takže ho můžeme v klidu zanedbat a máme krásný výsledek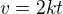

$v = 2kt$

Tedy rychlost lineárně narůstající.

Takže pokud někde uvidíme ten výraz 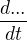$\frac{d...}{dt}$ znamená to přesně tenhle postup. Samozřejmě, pro každou funkci je jiná i její derivace, a pokud nedokážeme polohu vyjádřit jako funkci, nemůžeme přesně určit ani tu rychlost, ale v teoretické rovině je to takto. Není žádný důvot to nějak obcházet, nic tomu nechybí. Akorát že když chce člověk trochu porozumět fyzice, tak bez diferenciálního počtu to úplně nejde...

Vladimir9O · 16. 06. 2020 21:48

Hele, myslím, že pro účely toho, k ččemu to potřebuju, jsou takový věci zbytečná teorie... taky řezník, když bourá maso, nepočítá, s jakou přesně silou má uděřit a pod jakým úhlem, aby flákotu oddělil co nejvíce efektivně.

Nejsou třeba jiné vzorce, co mi udělají podobnou službu?

edison · 16. 06. 2020 22:11 — Editoval edison (16. 06. 2020 22:13)

No to záleží na okolnostech. Derivování a integrování má výhodu v univerzálnosti.

Prostě stačí vědět o co de a pak už se derivováním, nebo integrováním dostaneš ke vzorci, který si ti, co neumí integrovat a derivovat musí pamatovat:-)

A u věcí ze základky, na které ses tady zatím ptal, se dá úspěšně použít postup, co jsem popsal tady: ↑ edison:

pietro · 16. 06. 2020 22:12

Ano

MichalAld · 16. 06. 2020 22:56

↑ Vladimir9O:
To záleží na tom, k čemu to potřebuješ......

Žádné moc jiné vzorce nejsou....akorát se můžeš v úvahách omezit na konstantní rychlost, pak je v=s/t, případně rovnoměrně narůstající rychlost (konstantní zrychlení). To je taková ta středoškolská fyzika.

Případně se tím nemusíš zabývat vůbec, podobně jako ten řezník...stačí vědět, že rychlost je to, co ukazuje ručička tachometru.

Vladimir9O · 17. 06. 2020 10:02

vlado_bb napsal(a):
↑ Vladimir9O:Pri obvyklom znaceni je $\frac{dt}{ds}$ derivaciou casu podla drahy :)

https://wikimedia.org/api/rest_v1/media … cf57a65f8c tady je ale ds/dt.

Vladimir9O · 17. 06. 2020 10:05

MichalAld napsal(a):
↑ Vladimir9O:
To záleží na tom, k čemu to potřebuješ......

Žádné moc jiné vzorce nejsou....akorát se můžeš v úvahách omezit na konstantní rychlost, pak je v=s/t, případně rovnoměrně narůstající rychlost (konstantní zrychlení). To je taková ta středoškolská fyzika.

Případně se tím nemusíš zabývat vůbec, podobně jako ten řezník...stačí vědět, že rychlost je to, co ukazuje ručička tachometru.

mě v podstatě ty derivace a integrály přijdou - možná neopodstatněně - jako přespříliš složité.

vlado_bb · 17. 06. 2020 10:22

Vladimir9O napsal(a):
mě v podstatě ty derivace a integrály přijdou - možná neopodstatněně - jako přespříliš složité.

Zalezi od toho, ake ma clovek ambicie. Ak som sa naucil iba scitovat, moze sa mi nasobilka zdat prilis zlozita. Ale ak (napriklad) casto nakupujem vacsie pocty toho isteho tovaru, tak sa nasobit naucim. Podobne, ak chcem vediet zaklady fyziky (takmer cokolvek, co je za hranicou priamociareho pohybu konstantnou rychlostou), tak sa derivovat a integrovat naucim.

Vladimir9O · 17. 06. 2020 17:03

Dobře, a
A) je to obtížné?
B) pokud ne, jaký zdroj bys doporučil?

vlado_bb · 17. 06. 2020 18:31

↑ Vladimir9O:

A - podla mna nie, su v principe dve cesty. Pri prvej je mozne pozerat na difernencialny a integralny pocet ako na sustavu navodov a neuvazovat prilis o ich podstate. Takto sa asi da skor dostat k aplikovatelnym veciam, ale je to narocne na zapamatanie si znacneho mnozstva faktov a hlavne - clovek je pri prvom co len trochu netradicnom probleme v koncoch. Druhy sposob je venovat viac casu pochopeniu principov a potom vsetko zacne davat zmysel a navyse clovek oceni aj esteticku hodnotu infinitezimalneho poctu. Ako zaklad by som tu videl dokladne pochopenie pojmu limity funkcie v bode.

B - tato oblast je mimoriadne dobre pokryta literaturou, takze kazdy si moze vybrat material, ktory mu najviac vyhovuje. Takmer kazda univerzita ma svoje studijne materialy, mnohe aj viacero, existuje znacny pocet monografii zaoberajucich sa diferencialnym a integralnym poctom. Do konca mesiaca je napriklad volne dostupna vyborna Abbottova kniha https://link.springer.com/content/pdf/1 … 712-8.pdf, ale napriklad aj text https://is.muni.cz/el/1433/podzim2010/M … omenne.pdf je napisany jednoduch, ale pritom dokladne. Plus asi tisic dalsich moznosti.

Vladimir9O · 18. 06. 2020 08:11

No, když se na to tak podívám, a jestli tomu rozumím správně, tak ta derivace je vlastně způsob jak "transformovat vzorce".
Udělat z jednoho vzorce nějaký jiný, a je jedno, co přesně ten derivovaný prvek reálně "reprezentuje".

vlado_bb · 18. 06. 2020 08:42

↑ Vladimir9O:Ani nie. Derivacia funkcie v bode je rychlost zmeny tejto funkcie v danom bode.

misaH · 18. 06. 2020 10:29

↑ Vladimir9O:

Derivácia DRÁHY PODĽA ČASU je tzv okamžitá rýchlosť.

Základoškolské a stredoškolské vzorce mimo derivácií sa týkajú obmedzených podmienok, ako píše edison.

Prosím ťa, o čo ide?

Na akej si škole?

Chceš ísť na SŠ alebo na VŠ?

Alebo o čo teda?

Ťažko sa odpovedá, keď nie je známy účel.

Zjednodušiť vzorec? Čo to je?

Matematické Fórum

#1 16. 06. 2020 18:48

Okamžitá rychlost (derivace???)

#2 16. 06. 2020 19:11

Re: Okamžitá rychlost (derivace???)

#3 16. 06. 2020 19:13

Re: Okamžitá rychlost (derivace???)

#4 16. 06. 2020 19:15

Re: Okamžitá rychlost (derivace???)

#5 16. 06. 2020 19:22

Re: Okamžitá rychlost (derivace???)

#6 16. 06. 2020 21:48

Re: Okamžitá rychlost (derivace???)

#7 16. 06. 2020 22:11 — Editoval edison (16. 06. 2020 22:13)

Re: Okamžitá rychlost (derivace???)

#8 16. 06. 2020 22:12

Re: Okamžitá rychlost (derivace???)

#9 16. 06. 2020 22:56

Re: Okamžitá rychlost (derivace???)

#10 17. 06. 2020 10:02

Re: Okamžitá rychlost (derivace???)

vlado_bb napsal(a):

#11 17. 06. 2020 10:05

Re: Okamžitá rychlost (derivace???)

MichalAld napsal(a):

#12 17. 06. 2020 10:22

Re: Okamžitá rychlost (derivace???)

Vladimir9O napsal(a):

#13 17. 06. 2020 17:03

Re: Okamžitá rychlost (derivace???)

#14 17. 06. 2020 18:31

Re: Okamžitá rychlost (derivace???)

#15 18. 06. 2020 08:11

Re: Okamžitá rychlost (derivace???)

#16 18. 06. 2020 08:42

Re: Okamžitá rychlost (derivace???)

#17 18. 06. 2020 10:29

Re: Okamžitá rychlost (derivace???)

Zápatí