Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 06. 2020 18:50
- Vladimir9O

- Příspěvky: 104
- Reputace: -1
Akcelerace
Jakto že má průměrná a okamžitá akcelerace stejnej vzorec?
https://cs.wikipedia.org/wiki/Zrychlen%C3%AD
Offline
#4 17. 06. 2020 07:16
#6 17. 06. 2020 10:30
Re: Akcelerace
↑ Vladimir9O:Limita funkcie  v bode
v bode  je
je 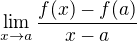 . V bode nula teda
. V bode nula teda 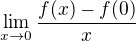 . Vo fyzikalnej situacii, ktoru popisujes, je
. Vo fyzikalnej situacii, ktoru popisujes, je  casovy usek lubovolne blizky nule, oznacuje sa
casovy usek lubovolne blizky nule, oznacuje sa 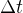 jemu zodpoveda prislusna zmena funkcie
jemu zodpoveda prislusna zmena funkcie  , teda
, teda 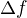 . U nas ide o rychlost, ktora sa obvykle oznacuje pismenom
. U nas ide o rychlost, ktora sa obvykle oznacuje pismenom  , teda
, teda 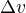 .
.
Offline
#7 17. 06. 2020 11:14 — Editoval LukasM (17. 06. 2020 11:15) Příspěvek uživatele LukasM byl skryt uživatelem LukasM. Důvod: Zavádějící
#8 17. 06. 2020 11:18
Re: Akcelerace
↑ Vladimir9O:
Já jen dodám, že vlastně přesně toto ti už rozepsal MichalAld zde. On začal u průměrné rychlosti za nějaký čas a pak ukázal, co se stane, když se ten čas bude neomezeně zkracovat, tedy "půjde k nule". To je právě výpočet limity a cesta od průměrné rychlosti k okamžité.
Toto je úplně to samé, akorát místo průměrné a okamžité rychlosti tady pracuješ s průměrným a okamžitým zrychlením. Logika výpočtu je přesně stejná, jediný rozdíl je v tom, že rychlost je změna dráhy a zrychlení změna rychlosti.
Offline
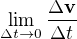 a
a 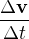 se na první pohled liší
se na první pohled liší