Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 06. 2020 07:18 — Editoval thorne (23. 06. 2020 07:21)
pomoc s důkazem
Pěkné ráno,
potřeboval bych ověřit (ne)správnost řešení následujícího příkladu.
Dokažte, že osoba A může zaplatit osobě B libovolnou celou částku v korunách, jestliže má k dispozici dostatečné množství pětikorun a osoba B dostatečně velké množství dvoukorun.
Takže jde o to dokázat, že výsledkem této rovnice může být jakékoli přirozené číslo 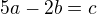 , a, b, c, jsou přirozená čísla.
, a, b, c, jsou přirozená čísla.
Mě napadlo to udělat nějak takhle (pomocí mat. indukce)
Děkuji za připadné příspěvky
Offline
- (téma jako vyřešené označil(a) thorne)
#4 23. 06. 2020 09:31
#5 23. 06. 2020 10:58
Re: pomoc s důkazem
↑ Ferdish:↑ vlado_bb:
Díky za tip, že nemusím rozlišovat sudá a lichá, zkusím se na to podívat. Pokud na něco přijdu, tak to sem hodím.
↑ vlado_bb:
Díky za ujištění
Offline
#6 23. 06. 2020 12:05
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: pomoc s důkazem
↑ thorne:
Myslenku mas v podstate dobrou. Nicmene vzhledem k tomu, ze chceme vedet, zda ma rovnice celociselne reseni pro kazde prirozene  , tak je systematictejsi rozlisovat pripady podle parametru
, tak je systematictejsi rozlisovat pripady podle parametru  .
.
(Tvuj prvni krok Pro sude a mi neprijde systematicky, protoze nikdo po nas nechce zjistovat, zda rovnice ma nejakou vlastnost pro kazde (sude) a.)
Napriklad by mi prislo prirozene postupovat takto:
1. Ukazu, ze pro c = 1, 2, 3, 4, 5 existuji vhodne dvojice a, b.
2. Pro c > 5 vezmu jeden z pripadu z kroku 1 a pridam dostatecne mnozstvi 5korun.
Nekdo jiny by mohl postupovat treba takto:
1. Ukazu, ze pro sude c lze najit vhodnou dvojici a, b tak, ze zvolim dostatecne velke sude a a nasledne odectu vhodny pocet dvoukorun.
2. Ukazu, ze pro liche c lze najit vhodnout dvojici a, b tak, ze zvolim dostatecne velke liche a a nasledne odectu vhodny pocet dvoukorun.
Urcite se daji najit i jine postupy. Mne slo o to ukazat, ze systematicke je rozlisovat pripady podle parametru  , nikoliv podle jinych parametru.
, nikoliv podle jinych parametru.
Offline
 :
: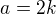 (k náleží N). Pak mám
(k náleží N). Pak mám . Za předpokladu, že je
. Za předpokladu, že je  strašně velké (tedy konstantní) a
strašně velké (tedy konstantní) a  procházejí postupně všechna přirozená čísla, tak postupně dostanu všechna sudá přirozená čísla menší než 10k.
procházejí postupně všechna přirozená čísla, tak postupně dostanu všechna sudá přirozená čísla menší než 10k.
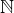 , jelikož je v
, jelikož je v  a
a 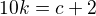
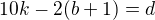 , d náleží
, d náleží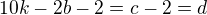 . Tedy jsem dostal číslo o 2 menší než
. Tedy jsem dostal číslo o 2 menší než