Matematické Fórum

denvan · 24. 06. 2020 21:12

Ahoj, prosím o pomoc s tímto úkolem z finanční matematiky. Pod zadáním přikládám i mé řešení, ale vím, že není správné, prosím tedy o radu, jak se posunout dál. Moc děkuji.

Pan Kropáček by si chtěl naspořit než půjde do důchodu na svůj vysněný zájezd do Antarktidy. V katalogu si zjistil cenu a počítá s tím, že ho takový zájezd se všemi náklady vyjde na 300 000 Kč. Peníze hodlá vkládat na spořící účet vždy 10. den v měsíci. Banka bude však vklady úročit vždy na konci kalendářního čtvrtletí s úrokovou mírou 1,6 %. První vklad uskuteční pan Kropáček 10. 7. 2020. Odchod do důchodu očekává k 1. 7. 2038. Jak vysokou částku musí na účet minimálně vkládat?

dny = 360 * (2038 – 2020) + (1 – 10) = 6471

n = 6471/90 = 71, 9 → 70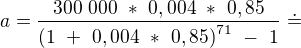

$a = \frac{300\ 000\ \ast\ 0,004\ \ast\ 0,85}{{(1\ +\ 0,004\ \ast\ 0,85)}^{71\ }-\ 1}\ \dot{=}$ 3743 Kč za čtvrt roku 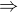$\Rightarrow$ 1248 Kč měsíčně

K mému řešení mám tyto poznámky: Oprava musí být ve výpočtu počtu období. Pokud se rozpočítá na čtvrt roky, tak by jich to celkem mělo dát 72, tedy dle standardu 30E/360 6480 dní. To první období sice není celé, ale počítat se musí. Proběhne celkem 72 úročení. A vlastně i ta částka, která se za to první čtvrtletí na účtu naspoří, je stejná jako v každém jiném čtvrtletí. V čem se ale jednotlivá období liší, je to, kolikrát z nich celkem jde úrok. Poté je potřeba upřesnit, jak z částky 3743 Kč za čtvrtletí získáme částku potřebnou za jeden měsíc, jelikož se nejedná o triviální krok.

Já s tím bohužel hnout neumím. Předem děkuji za rady, ráda někomu za pomoc ke správnému postupu i zaplatím, jen už to potřebuji mít konečně za sebou. Děkuji.

denvan · 24. 06. 2020 21:57

Předělala jsem to takto, ale vůbec nevím, jestli jsem na správné cestě. //forum.matweb.cz/upload3/img/2020-06/28576_received_580739196170557.jpeg

kastanek

↑ denvan:
Ten výpočet období (a vlastně úplně všeho) máš nějak komplikovaný. Je to 18 let a tedy 72 ukončených čtvrtletí. Dále je tam nepřesné zadání, zda je úroková míra roční či čtvrtletní a zda je čistá či hrubá.
Pokud budu předpokládat, že je (tak jak je obvyklé) roční (p. a.) a hrubá, pak je hrubý čtvrtletní úrok 0,4 % a čistý úrok po odečtení 15% daně 0,34 %, takže kvocient je 1,0034. A teď už jen dosadit:
$s=a_0q\frac{q^n-1}{q-1}$
$a_0=\frac{s(q-1)}{q(q^n-1)}$
$a_0=\frac{300000\cdot (1{,}0034-1)}{1{,}0034\cdot (1{,}0034^{72}-1)}\doteq 3672$
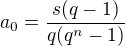
To je spořená částka za čtvrtletí, takže měsíčně to je 1224 Kč.

denvan · 25. 06. 2020 10:11

Moc děkuji, ale jak jsem psala, bylo mi od vyučujícího řečeno, že výpočet měsíční částky ze čtvrtletní není triviální krok, ve svém prvním řešení jsem to také pouze vydělila třemi a evidentně to dobře není. Přitom tím vypočítáme, kolik má za čtvrtletí vkládat, ne? A jelikož částku vkládá stále stejnou, nechápu, proč by se to nemohlo třemi vydělit.

surovec · 25. 06. 2020 16:19

↑ denvan:
Řekl bych, že vyučující se v tom moc nevyzná. Pokud se úročí na konci čtvrtletí, je úplně fuk, jak tam tu čtvrtletní částku nasázíš, jestli třikrát stejnou, nebo desetkrát pokaždé jinou. ↑ kastanek: to má dobře.

nejsem_tonda

↑ surovec:
Tentokrat si myslim, ze nemas pravdu (ani kastanek). Podle me teda bance zalezi na tom, zda tam penize mam cele ctvrtleti, nebo treba jen posledni dva tydny z celeho ctvrtleti. Podle toho mi da jenom primerenou cast uroku.

Denvan, ve svem druhem prispevku to pocitas v podstate spravne. Vypocet obdobi mas podle me taky spravne, ani si nemyslim, ze jde pocitat nejak (vyrazne) jednoduseji.

Pro me jedina otazka je, co banka presne vyjadruje tim, kdyz rekne, ze urok je 1.6% rocne. Budu ted uvazovat vsechno bez 15% dane. Potom porad vidim dve moznosti, jak k vypoctum pristupovat a oba davaji svym zpusobem smysl.

Moznost A: Banka tim vyjadruje to, ze kdyz na ucte po dobu jednoho roku necham x Kc, budu tam na konci roku mit 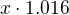$x\cdot1.016$ Kc. Pokud to takto je, tak potom za jedno ctvrtleti pripisujou $\sqrt[4]{1.016}-1$ nasobek vkladu.

Urok za 80 dni potom vychazi: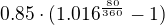
$0.85\cdot (1.016^{\frac{80}{360}}-1)$

Moznost B: Banka tim vyjadruje to, ze kdyz na ucet vlozim x Kc a po kazdem ctvrtleti si z uctu vezmu uroky, budu tam mit na konci roku 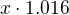$x\cdot1.016$ Kc.

Pokud by to bylo takto, tak bych uroky za 80 dni pocital presne stejne jako to delas ty, tj. 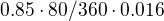$0.85\cdot 80/360 \cdot 0.016$

Rozdil mezi moznosti A a B vychazi strasne maly, ale jde spis o princip, jak k vypoctu pristupovat. Pro kontrolu mi pri zpusobu A vychazi 1226,78 Kc a pri zpusobu B mi vychazi 1225,85 Kc jako mesicni vklad (kdyz chceme, aby pan Vomacka vkladal kazdy mesic stejnou castku, coz je velmi prirozeny pozadavek).

denvan · 26. 06. 2020 17:53

↑ nejsem_tonda:

Super, moc děkuji.
Doptala jsem se učitele a kde je to relevantní, tak se má zohlednit daň z úroku (úroková míra je klasicky roční), takže tvá možnost B.

surovec · 26. 06. 2020 20:40

↑ nejsem_tonda:
Já bych řekl, že v reálu, v bance, to probíhá tak, jak jsem psal, kdysi jsem se na to i v bance ptal. V praxi se (skoro vždy) uvádí roční úroková míra a ta se přepočítává na konkrétní úrokovací období prostým dělením úroku, takže v tomto případě by (hrubý) úrok při půlročním úrokovacím období byl 0,8, při měsíčním 1,6/12, při denním 1,6/360 atd. A pokud se úrok připisuje na konci úrokovacího období, tak se úročí ta aktuální částka, která tam v tom okamžiku je, to je konec konců smysl toho úrokovacího období, jinak by se automaticky mohlo všechno úrokovat spojitě...

nejsem_tonda · 26. 06. 2020 22:17

↑ surovec:
Tak napriklad Creditas uroci "skoro spojite" - nejmensi jednotka je jeden den. Uroky pripisuji jednou mesicne, ale kdyz jsi tam dal penize den pred urocenim, zapocitaji skutecne jenom jeden den, nikoliv cely mesic. Tedy presne podle toho, co popisuju v moznosti B: 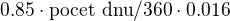$0.85\cdot \text{pocet dnu}/360 \cdot 0.016$ . Teda mozna to deli skutecnym poctem dnu v roce, to uz opravdu zjistene nemam.

surovec

↑ nejsem_tonda:
Ale ty tu zaměňuješ dvě rozdílné věci: frekvenci připisování úroku a "úrokovací období" (proto jsem to v předchozím příspěvku vytučnil, abych na to upozornil). U toho kreditas připisují úrok jednou měsíčně, ale úrokovací období je den (u čehož je mimochodem opravdu standard 360 bankovních dnů za rok).
V této úloze je však formulace "Banka bude však vklady úročit vždy na konci kalendářního čtvrtletí", z čehož vyplývá, že zde je úrokovací období čtvrtletí a nikoliv den. Neboli zde splývá "frekvence připisování úroku" s "úrokovacím obdobím".

Matematické Fórum

#1 24. 06. 2020 21:12

Finanční matematika - spoření

#2 24. 06. 2020 21:57

Re: Finanční matematika - spoření

#3 24. 06. 2020 22:18 — Editoval kastanek (24. 06. 2020 22:20)

Re: Finanční matematika - spoření

#4 25. 06. 2020 10:11

Re: Finanční matematika - spoření

#5 25. 06. 2020 16:19

Re: Finanční matematika - spoření

#6 26. 06. 2020 14:29 — Editoval nejsem_tonda (26. 06. 2020 14:32)

Re: Finanční matematika - spoření

#7 26. 06. 2020 17:53

Re: Finanční matematika - spoření

#8 26. 06. 2020 20:40

Re: Finanční matematika - spoření

#9 26. 06. 2020 22:17

Re: Finanční matematika - spoření

#10 27. 06. 2020 13:54 — Editoval surovec (27. 06. 2020 13:55)

Re: Finanční matematika - spoření

Zápatí