Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 29. 06. 2020 16:26
Re: Nerovnost
Jj napsal(a):
↑ Dacu:
Hezký den.
Pokud vím, tak komplexní čísla nelze uspořádat podle velikosti. Takže co se úlohou myslí?
Ahoj,
Je nerovnost  ekvivalentní rovnici
ekvivalentní rovnici 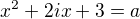 kde
kde  ?
?
Vše nejlepší,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#8 30. 06. 2020 12:58
Re: Nerovnost
jarrro napsal(a):
↑ Dacu:prečo by neexistovalo?
Ahoj,
Je nerovnost  ekvivalentní rovnici
ekvivalentní rovnici 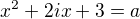 kde
kde  a tak existují řešení!
a tak existují řešení!
----------------------------------------------------------
Co vyplývá z režimu řešení uvedeného Iaszkym s  a zaroven
a zaroven  ???
???
Vše nejlepší,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#10 30. 06. 2020 13:18
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Nerovnost
Dacu napsal(a):
Nerozumím!Říkáte, že neexistují žádná řešení?
Nie, tvoja nerovnica nemá riešienie ani na obore komplexných čísel. Dôvod ti už prezradil kolega ↑ Jj:.
Wolfram ti potvrdí to isté: Odkaz. Ako inžinier si pravdepodobne o tomto takmer všemocnom nástroji počul. A keby aj nie (nech už je dôvod akýkoľvek), tak ste sa práve zoznámili :-)
Offline
#11 30. 06. 2020 13:20
Re: Nerovnost
↑ vlado_bb:
O jakém řešení mluvíte?
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#12 30. 06. 2020 13:26
Re: Nerovnost
Ferdish napsal(a):
Dacu napsal(a):
Nerozumím!Říkáte, že neexistují žádná řešení?
Nie, tvoja nerovnica nemá riešienie ani na obore komplexných čísel. Dôvod ti už prezradil kolega ↑ Jj:.
Wolfram ti potvrdí to isté: Odkaz. Ako inžinier si pravdepodobne o tomto takmer všemocnom nástroji počul. A keby aj nie (nech už je dôvod akýkoľvek), tak ste sa práve zoznámili :-)
Z „WolframAlpha“ přečtěte:
Odkaz.
Vše nejlepší,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#13 30. 06. 2020 16:24 — Editoval jarrro (02. 03. 2021 11:42)
Re: Nerovnost
↑ Ferdish:prečo by nemala riešenie? aj operovanim s komplexnými číslami možno získat reálne číslo.


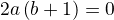


teda 
MATH IS THE BEST!!!
Offline
#14 30. 06. 2020 16:52
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Nerovnost
Ten prechod od druhého riadka k tretiemu sa mi nejako nepozdáva...pochopil som že si použil prepis 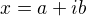 , ale to umocňovanie mi nesedí. Nemám však poruke pero ani papier aby som si to overil vlastným výpočtom.
, ale to umocňovanie mi nesedí. Nemám však poruke pero ani papier aby som si to overil vlastným výpočtom.
Offline
#15 30. 06. 2020 17:12 — Editoval Dacu (30. 06. 2020 17:12)
Re: Nerovnost
jarrro napsal(a):
↑ Ferdish:prečo by nemala riešenie? aj operovanim s komplexnými číslami možno získat reálne číslo.
teda
Hello,
You considered 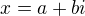 where
where  .... Very good!Isn't it easier as I said?
.... Very good!Isn't it easier as I said?
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#17 30. 06. 2020 18:37
Offline
#19 30. 06. 2020 19:27
Re: Nerovnost
Podstata byla řečena hned na začátku:
Pokud vím, tak komplexní čísla nelze uspořádat podle velikosti. Takže co se úlohou myslí?
Jde o to, že je nutno zvolit nějaký úhel pohledu, kdy symbol < začne dávat smysl i s komplexními čísly, tedy odpovědět na citovanou otázku.
WA odpověď nezná a tak odpoví že nic:
https://www.wolframalpha.com/input/?i=x … ix%2B3%3C0
Když mu nějaký smysluplný pohled podstrčíme, nějaké řešení najde:
https://www.wolframalpha.com/input/?i=x … Da%2Ca%3C0
Kdyby se mu podstrčil jiný úhel pohledu, dá určitě i jinou odpověď.
Offline