Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 30. 06. 2020 16:30
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Systém diferenciálních rovnic
Listen to me, my friend.
It is apparent that your mother tongue is not Czech nor Slovak and your communication via translator does not seem to work very well. Otherwise you would already understand what we were trying to tell you.
It is essential for you to understand how the things work around here. First, it is convenient to read through our forum rules. Unfortunately I have no knowledge about our rules being available in other than Czech language. No wonder - 99% of active members here are Czechs or Slovaks or at least Czech/Slovak fluent speakers so there was no need for variations in other languages. If you want I can translate them for you (much better than the software you use for translation - believe that).
I hope you understand this text, since I am not sure if you speak English at all...
Offline
#3 30. 06. 2020 16:52
Re: Systém diferenciálních rovnic
Ferdish napsal(a):
Listen to me, my friend.
It is apparent that your mother tongue is not Czech nor Slovak and your communication via translator does not seem to work very well. Otherwise you would already understand what we were trying to tell you.
It is essential for you to understand how the things work around here. First, it is convenient to read through our forum rules. Unfortunately I have no knowledge about our rules being available in other than Czech language. No wonder - 99% of active members here are Czechs or Slovaks or at least Czech/Slovak fluent speakers so there was no need for variations in other languages. If you want I can translate them for you (much better than the software you use for translation - believe that).
I hope you understand this text, since I am not sure if you speak English at all...
I understood!I'm very sorry to bother you, but I want to understand math as well as possible ... Thank you very much for your understanding!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#4 01. 07. 2020 17:15
Re: Systém diferenciálních rovnic
Hello all,
No one is answering?The proposed problem may seem strange, but I think it has a simple solution, because it requires solving a system of differential equations with modules ...
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#5 02. 07. 2020 06:56 — Editoval jarrro (02. 07. 2020 06:56)
Re: Systém diferenciálních rovnic
since 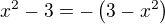 the given system can be satisfied if and only if
the given system can be satisfied if and only if 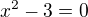 which satisfy only two numbers x.
which satisfy only two numbers x.
Diffferential equation and their systems should be satisfied on some nondegenerated opn interval. So this system cannot be satisfied.
I hope I dont male a mistake.
MATH IS THE BEST!!!
Offline
#6 02. 07. 2020 13:46 — Editoval krakonoš (02. 07. 2020 13:55) Příspěvek uživatele krakonoš byl skryt uživatelem jelena. Důvod: OT, viz samostatné téma
#8 02. 07. 2020 16:59 — Editoval vanok (02. 07. 2020 17:00) Příspěvek uživatele vanok byl skryt uživatelem jelena. Důvod: OT, viz samostatné téma
#9 02. 07. 2020 17:52 — Editoval krakonoš (02. 07. 2020 17:52) Příspěvek uživatele krakonoš byl skryt uživatelem jelena. Důvod: OT, viz samostatné téma
#10 02. 07. 2020 22:58 — Editoval vanok (02. 07. 2020 23:01) Příspěvek uživatele vanok byl skryt uživatelem jelena. Důvod: OT, viz samostatné téma
#11 02. 07. 2020 23:27 — Editoval misaH (02. 07. 2020 23:29) Příspěvek uživatele misaH byl skryt uživatelem jelena. Důvod: OT, viz samostatné téma
#12 02. 07. 2020 23:43 Příspěvek uživatele Ferdish byl skryt uživatelem jelena. Důvod: OT, viz samostatné téma
#13 03. 07. 2020 07:37 — Editoval krakonoš (03. 07. 2020 07:38) Příspěvek uživatele krakonoš byl skryt uživatelem jelena. Důvod: OT, viz samostatné téma
#14 03. 07. 2020 10:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Systém diferenciálních rovnic
Zdravím, OT debata o národních matematických fórech je oddělena do samostatného tématu, dle zájmu pokračujte, prosím, v tématu, nebo si založte vlastní v příslušné sekci. Děkuji.
Offline
#17 08. 07. 2020 09:30 — Editoval Dacu (08. 07. 2020 13:44)
Re: Systém diferenciálních rovnic
Hello,
From 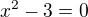 results
results 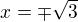 and so what are the values of the functions
and so what are the values of the functions 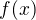 and
and  for
for 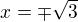 ?
?
Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#21 08. 07. 2020 13:42
Re: Systém diferenciálních rovnic
I think that one solution could be  and
and  .
.
Please kindly prove to me that the above solution is not correct!Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#24 10. 07. 2020 06:07 — Editoval Dacu (10. 07. 2020 06:18)
Re: Systém diferenciálních rovnic
Bati napsal(a):
↑ Dacu:
Let. Then
for all
, but
only if
or
.
Hello,
I think you meant that 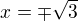 ...What other values can
...What other values can 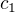 and
and  take and so what are all the solutions of nonlinear system of the differential equations?Thank you very much!
take and so what are all the solutions of nonlinear system of the differential equations?Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#25 10. 07. 2020 06:15 — Editoval Dacu (10. 07. 2020 06:18)
Re: Systém diferenciálních rovnic
Hello,
Bati has a different opinion ... Is it wrong what Bati says?!?!Thank you very much!
From the "WolframAlpha" reading:
Odkaz.
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline