Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 08. 07. 2020 20:44

Marcia24
Příspěvky: 253
Reputace:   0 
 

Dosazení do výrazu

Dobrý den, mohla bych se prosím zeptat, jak se sem dosadí? Odkud se vezmou ty zažlucené členy? Moc děkuji
//forum.matweb.cz/upload3/img/2020-07/33837_V%25C3%25BDst%25C5%2599i%25C5%25BEek.PNG
Zdroj: http://leteckaposta.cz/937495834

Offline

  • (téma jako vyřešené označil(a) Marcia24)

#2 08. 07. 2020 23:08

jelena
Jelena
Místo: Opava
Příspěvky: 30020
Škola: MITHT (abs. 1986)
Pozice: plním požadavky ostatních
Reputace:   100 
 

Re: Dosazení do výrazu

Zdravím,

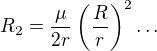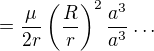děkuji za zprávu v tématu. Když do posledního řádku na scanu dosadím po druhém $=$ $R_2=\frac{\mu}{2r}\(\frac{R}{r}\)^2\ldots$ (zapisuj jen část podstatnou pro úpravu z dotazu) a rozšířím výraz $a^3$, máme $=\frac{\mu}{2r}\(\frac{R}{r}\)^2\frac{a^3}{a^3}\ldots$, mohu před znak integrálu vytknout konstanty tak, jak je v zápisu (ještě před žlutou části): $=\frac{\mu}{2a}\(\frac{R}{a}\)^2\ldots$.
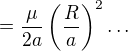že je rozepsáno na 2 zlomky (zažluceno), spíše pro přehlednost úprav. Pomůže rozepsat podrobně dosazení 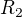$R_2$, rozšíření a až potom vytknutí konstant před integrál. Stačí tak? Děkuji.

Offline

 

#3 09. 07. 2020 04:12

Marcia24
Příspěvky: 253
Reputace:   0 
 

Re: Dosazení do výrazu

↑ jelena:
Moc děkuji

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson