Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 25. 07. 2020 08:44
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Fermatova Velká Věta
↑↑ Dacu:
How does from the fact that 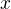 ,
,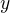 are natural numbers follows that
are natural numbers follows that  ,
, are natural numbers?
are natural numbers?
"Máte úhel beta." "No to nemám."
Offline
#27 25. 07. 2020 12:30
Re: Fermatova Velká Věta
Dear colleagues, I certainly do not want to interfere with this discussion, however, Dacu - if you are sure you have an alternative proof of FLT, I strongly recommend to submit it into a suitable journal, in this case probably to the Annals of Mathematics.
Offline
#28 25. 07. 2020 18:24
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Fermatova Velká Věta
It can be useful excercise to find weak spots in presented proofs, so we can continue this discussion.
"Máte úhel beta." "No to nemám."
Offline
#29 26. 07. 2020 08:16
Re: Fermatova Velká Věta
Hello all,
Dear users of the forum, I will soon show that from variant "2) 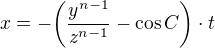 and
and 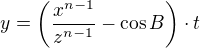 where
where  with
with 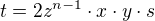 where
where  and
and  ". results
". results  .
.
For personal reasons I have to postpone the next post. Thank you very much for your understanding!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#30 26. 07. 2020 22:58
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Fermatova Velká Věta
↑ Dacu:
Firstly you have to proove that 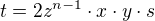 and that
and that  .
.
"Máte úhel beta." "No to nemám."
Offline
#31 27. 07. 2020 07:11 — Editoval Dacu (27. 07. 2020 07:19)
Re: Fermatova Velká Věta
check_drummer napsal(a):
↑ Dacu:
Firstly you have to proove thatand that
.
Hello,
Because in 5) 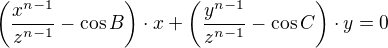 we have
we have  and
and  , then it follows that the equation
, then it follows that the equation 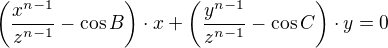 is a Diophantine equation with rational coefficients.
is a Diophantine equation with rational coefficients.
----------------------------------------
Example of Diophantine equation with rational coefficients:
Solve the Diophantine equation in the set of integer numbers  .
.
Solution: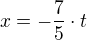 and
and  where
where and
and 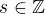 .
.
I am waiting for the following questions ...
Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#32 27. 07. 2020 20:45
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Fermatova Velká Věta
↑ Dacu:
Hi,
1) why do both inequalities hold?
and why it is important that they hold?
2) Why it is important that we got Diophantine equation?
"Máte úhel beta." "No to nemám."
Offline
#33 28. 07. 2020 14:03
Re: Fermatova Velká Věta
check_drummer napsal(a):
↑ Dacu:
Hi,
1) why do both inequalities hold?
and why it is important that they hold?
2) Why it is important that we got Diophantine equation?
Hello,
1) Correction: and
and 
2) For demonstration .... and in fact 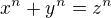 is a Diophantine equation ...
is a Diophantine equation ...
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#34 28. 07. 2020 20:46 — Editoval check_drummer (28. 07. 2020 20:59)
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Fermatova Velká Věta
↑ Dacu:
So why does the inequalities with absolute values hold?
Edit: I see inequality "<1" - because we are subtracting numbers that are in interval (0;1), but I don't see inequality "<0" ie why those numbers are not equal.
"Máte úhel beta." "No to nemám."
Offline
#35 29. 07. 2020 07:02 — Editoval Dacu (29. 07. 2020 07:13)
Re: Fermatova Velká Věta
check_drummer napsal(a):
↑ Dacu:
So why does the inequalities with absolute values hold?
Edit: I see inequality "<1" - because we are subtracting numbers that are in interval (0;1), but I don't see inequality "<0" ie why those numbers are not equal.
Hello,
I repeat:
"From 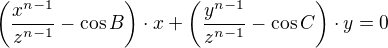 the following possibilities result:
the following possibilities result:
1) 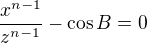 and
and 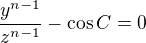 .
.
2) 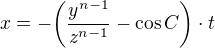 and
and 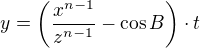 where
where  with
with 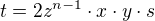 where
where  and
and  .
.
Which of the two possibilities can exist, 1) or 2)?"
----------------------------------------------------------------
What inequality are you talking about, what equality of numbers are you talking about?Thank you very much!
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#36 02. 08. 2020 09:30
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Fermatova Velká Věta
↑ Dacu:
So - you dont know the answer and this is the question for the whole forum?
Why in 2) this must hold: 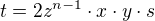 ,
,  ?
?
"Máte úhel beta." "No to nemám."
Offline
#37 04. 08. 2020 06:31 — Editoval Dacu (04. 08. 2020 06:32)
Re: Fermatova Velká Věta
check_drummer napsal(a):
↑ Dacu:
So - you dont know the answer and this is the question for the whole forum?
Why in 2) this must hold:,
?
Hello,
I reformulate variant 2):
2) 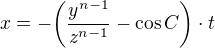 and
and 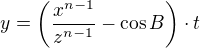 where
where 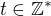 and
and  .
.
Let 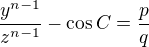 and
and 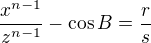 two irreducible fractions , then there are the following possibilities:
two irreducible fractions , then there are the following possibilities:
a)  ,
,  ,
,  and
and  where
where  with
with  .
.
b)  ,
,  ,
,  and
and  where
where  where
where  .
.
Because  and
and 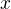 ,
, 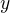 ,
, 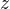 must have no common divisors, then it is necessary that
must have no common divisors, then it is necessary that 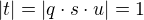 and so
and so  which contradicts
which contradicts  .
.
All the best,
Dacu
"Don't worry about your difficulties to math.I assure you that mine are even bigger! ” Albert Einstein
Offline
#38 05. 08. 2020 20:56
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Fermatova Velká Věta
↑ Dacu:
So you are trying to prove that variant 2) cannot hold, right? So I have two questions:
I) How do you know that  is whole number and not rational number? (From what fact daes it follow?)
is whole number and not rational number? (From what fact daes it follow?)
II) Why other variants except a) and b) cannot hold - ie that p,q have the same sign?
III) Why eg in a) equality  holds?
holds?
Thank you.
"Máte úhel beta." "No to nemám."
Offline
