Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Stejnoměrná konvergence (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 09. 2020 17:58
Stejnoměrná konvergence
Dobrý den,
můžu se zeptat, jak přijdu na to, že (nx)/(1+n^2x^2) konverguje stejnoměrně na intervalu (1,+infty), ale nekonverguje stejnoměrně na (0,+infty)?
Zkouším to přes limsup pravidlo, ale nemůžu s tím hnout. Díky moc!
Offline
- (téma jako vyřešené označil(a) Tom01)
#3 16. 09. 2020 22:16 — Editoval krakonoš (17. 09. 2020 00:21)
Re: Stejnoměrná konvergence
↑ vlado_bb:↑ Tom01:
Ahoj.
Neplatí že funkce budou stejnoměrně konvergovat na (1; nekonečno),když to bude stejnoměrně konvergovat na každém uzavřeném intervalu, který je jeho podmnožinou? Pak by vlastně šlo uvažovat ve smyslu Diniho věty, jestli nepřehlížím nějaký nedostatek, na intervalech[1+epsilon ;K].Aspoň lokálně by to na tom intervalu (1; nekonečno) mělo pak fungovat.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#4 17. 09. 2020 03:55 — Editoval vlado_bb (17. 09. 2020 09:15)
Re: Stejnoměrná konvergence
krakonoš napsal(a):
↑ vlado_bb:↑ Tom01:
Ahoj.
Neplatí že funkce budou stejnoměrně konvergovat na (1; nekonečno),když to bude stejnoměrně konvergovat na každém uzavřeném intervalu, který je jeho podmnožinou?
Ak si mala na mysli uzavrete ohranicene intervaly, tak protipriklady su napriklad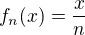
alebo
Ak aj neohranicene, tak protiprikad moze byt
Offline
#5 17. 09. 2020 10:49
Re: Stejnoměrná konvergence
↑ vlado_bb:
Takto by to fungovalo asi jen pro lokální stejnoměrnou konvergenci.
Budeme asi muset vyjít z toho, že jednotlivé funkce mají maxima pro x=1/n, čili pro x>1 už budou všechny funkce f_n(x) klesající a porovnáme-li  s
s  dosáhneme stejnoměrné konvergence vlastně podle definice.Aspoň já to tak vidím.
dosáhneme stejnoměrné konvergence vlastně podle definice.Aspoň já to tak vidím.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#6 17. 09. 2020 19:57
Re: Stejnoměrná konvergence
Selským rozumem je to jasné, protože v okolí bodu x=0 funkce konverguje "zboku" a né "shora", nejvyšší bod funkce zůstává pořád stejný, a žádnou volbou n ho nedokážeme snížit.
Stačí to jen vhodně matematicky popsat (tj. vyjádřit tu maximální hodnotu, které funkce nabývá a ukázat, že v okolí bodu x=0 ji žádnou volbou n nedokážeme snížit (že na n nezávisí).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Stejnoměrná konvergence (TOTO TÉMA JE VYŘEŠENÉ)

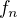 .
.