Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Náhodné procesy - střední hodnota a autokovarianční matice
#1 28. 09. 2020 19:56 — Editoval Tom01 (28. 09. 2020 20:09)
Náhodné procesy - střední hodnota a autokovarianční matice
* Edit: Pardon, v názvu nemá být autokovarianční matice, ale funkce
Ahoj,
můžu se zeptat, jak mám postupovat při řešení následujícího zadání?
Nechť X je náhodná veličina, která má rovnoměrné rozdělení na intervalu <0,pi>. Definujeme náhodný proces {Y(t) = t , t je z N}
Y(t) = t + cos(tX), t = 1,2,...
Máme určit střední hodnotu a autokovarianční funkci procesu.
X je z rovnoměrného spojitého rozdělení, které má střední hodnotu = 1/2*(b-a) = 1/2*(pi-0) = pi/2?
Mám pocit, že míchám jablka s hruškama. :D Nevím, jestli mi E(X) pomůže s výpočtem E(Y(t)). Někde jsem viděl, že to má vyjít t ... Ale uniká mi proč.
Y(t) = t + cos(t*X), kde tedy cos(t*X) bude nabývat hodnot mezi 0 a 1 (včetně). Ale jak z toho teď získat tu informaci o E(Y(t))?
Díky moc za každou radu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Náhodné procesy - střední hodnota a autokovarianční matice

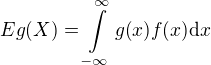 kde f je hustota náhodnej premennej X.
kde f je hustota náhodnej premennej X.