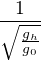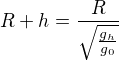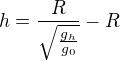Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 10. 2020 20:25 — Editoval Luky223 (15. 10. 2020 20:26)
Fyzika zrýchlenie voľného pádu
Dobrý deň,
Pomohol by mi prosim niekto ako vyjadrit neznamu z tohto vzorca prosim?
Potrebné je vypočítať "h" 
Viem akurát dostat g0 pod gh a odmocnit a dalej si neviem poradiť čo s tým..
Ďakujem za odpoveď..
Offline
- (téma jako vyřešené označil(a) Luky223)
#5 15. 10. 2020 21:32 — Editoval Ferdish (15. 10. 2020 21:35)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Fyzika zrýchlenie voľného pádu
↑ Luky223: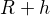 treba brať ako celok. Ak ním chceš násobiť, musí byť v zátvorke.
treba brať ako celok. Ak ním chceš násobiť, musí byť v zátvorke.
Práve preto som chcel, nech si ho nahradíš jedným písmenom a po prekonaní problematickej časti úpravy by si sa vrátil naspäť k pôvodnému označeniu.
Offline
#6 15. 10. 2020 21:39 — Editoval misaH (15. 10. 2020 21:46)
- misaH
- Příspěvky: 13467
Re: Fyzika zrýchlenie voľného pádu
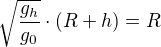
si mal mať a naozaj najprv využiť radu od Ferdiša (zdravím).
Myslel to dobre, miesto zátvorky dať ľubovoľné písmeno, vyjadriť ho a až následne napísať miesto neho pôvodné R+h.
Na zátvorky pozor, nesmú sa hocikedy len tak vynechať...
5(a+b) je niečo úplne iné ako 5a+b.
Offline
#7 16. 10. 2020 18:11
Re: Fyzika zrýchlenie voľného pádu
No skúšal som to aj s písmenkom "a" ale stále mi robí problém to odvodiť
Ak by som postupoval tak ako to napisal misaH
v ďalšom kroku by som roznasobil zatvorku a ostalo by mi to takto: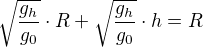
Niesom si istý či som to správne vynásobil, ale stále neviem osamostatnit  ktoré potrebujem vypočítat
ktoré potrebujem vypočítat
Offline
#9 16. 10. 2020 18:30
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Fyzika zrýchlenie voľného pádu
↑ Luky223:
Áno, je to správne. Prípadne sa môže výsledný vzťah ďalej upraviť.
Offline
 , budeš vedieť pokračovať?
, budeš vedieť pokračovať?