Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » modularni umocneni (TOTO TÉMA JE VYŘEŠENÉ)
#4 10. 06. 2009 21:01
Re: modularni umocneni
Já vím, že je to špatně :-)
Jinak jsem si domyslel, že když má být výsledek modulo 8, tak mohu každý činitel udělat modulo 8 a pak to bude 1*1*1*.... :-)
Asi špatně, jen pokus :-D Taky jsem napsal "podle mě" :D
oo^0 = 1
Offline
#9 11. 06. 2009 10:29 — Editoval musixx (11. 06. 2009 10:36)
Re: modularni umocneni
Uvaha od ttopi je v poradku. Kazde cinitele si mohu upravovat pomoci modulu, tedy je  .
.
Dale lze vyuzit treba Eulerovu vetu  , kde
, kde 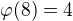 , tedy
, tedy 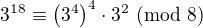 nebo treba rovnost
nebo treba rovnost 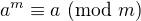 , tedy
, tedy 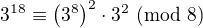 .
.
EDIT: zejmena ta Eulerova veta je pomerne silny nastroj, protoze nam rika, jakym modulem muzeme "snizovat" exponent. Jde totiz o to, najit vhodne vyjadreni exponentu modulo 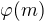 , kde m je puvodni modulo.
, kde m je puvodni modulo.
EDIT2: Je treba si totiz uvedomit, ze v zakladech mocnin lze libovolne cislo nahradit cislem s tim kongruentnim, ale v exponentech ne. Proc? Laicky receno, na prvni pohled jsou to cisla jako cisla, ale na druhy pohled, ta cisla v zakladech mocnin jsou reprezentatni zbytkovych trid, zatimco ta cisla v exponentech jsou pouze symboly, ktere pouzivame pro zkraceny zapis nekolika nasobeni. Proto ten odlisny pristup. Kdyz si tohle clovek uvedomi, jsou veci hned jasnejsi.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » modularni umocneni (TOTO TÉMA JE VYŘEŠENÉ)
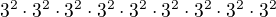 což je jako
což je jako  což je modulo 8 rovno 1. Ale ruku do ohně za to nedám, jen mě to napadlo.
což je modulo 8 rovno 1. Ale ruku do ohně za to nedám, jen mě to napadlo.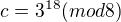
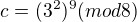
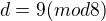


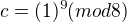

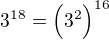 ? To ses sekl a má tam být ^9 nebo je to v rámci té modulární aritmetiky tak?
? To ses sekl a má tam být ^9 nebo je to v rámci té modulární aritmetiky tak?