Matematické Fórum

Proch · 18. 10. 2020 10:59

Dobrý den,
narazil jsem narazil jsem na zajímavou úlohu, kdy mám rozhodnout o konvergenci nebo divergenci řady, ale nevím jak výpočet dokončit pro a<0 a a=2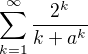
$\sum_{k=1}^{\infty }\frac{2^{k}}{k+a^{k}}$
Řekl jsem si že by se tu nechalo použít D'Alamberovo kritérium pokud a>0
Z toho mi vyšlo
$\lim_{k\to\infty }\frac{2^{k+1}}{k+1+a^{k+1}}*\frac{k+a^{k}}{2_{k}}=\lim_{k\to\infty }\frac{2k+2a^{k}}{k+1+a^{k+1}}=\lim_{k\to\infty }2*\frac{a^{k}}{a^{k}}*\frac{\frac{k}{a^{k}}+1}{\frac{k}{a^{k}}+\frac{1}{a^{k}}+a}=\lim_{k\to\infty }2*1*\frac{1}{a}=\frac{2}{a}$
Z toho mi tedy plyne, že pokud
2/a<1 --> tak řada konverguje, tedy konverguje v intervalu (2; $\infty$ )
2/a>1 --> tak řada diverguje, tedy diverguje v intervalu (0; 2)
měl bych dál ošetřit případ pro 0
pro 0 tedy platí
a=0 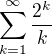$\sum_{k=1}^{\infty }\frac{2^{k}}{k}$
použiju srovnávací kritérium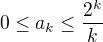
$0\le a_{k}\le \frac{2^{k}}{k}$
aplikuji znova D'A kritérium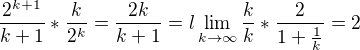
$\frac{2^{k+1}}{k+1}*\frac{k}{2^{k}}=\frac{2k}{k+1}=l\lim_{k\to\infty }\frac{k}{k}*\frac{2}{1+\frac{1}{k}}=2$ z toho mi plyne, že řada diverguje

Bati · 18. 10. 2020 14:28

Jdes na to zbytecne slozite. Nutna podminka konvergence rady je, ze cleny konveruji k nule. Protoze $k$ je asymptoticky zanedbatelne vzhledem k 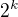$2^k$ , okamzite dostavas ze nutne $|a|>2$ . Konvergence pak plyne ze srovnavaciho kriteria, protoze $2^k>k$ pro dostatecne velke $k$ .

Proch · 19. 10. 2020 16:58

Děkuji, mělo mě to napadnout.

Matematické Fórum

#1 18. 10. 2020 10:59

Nekonečné řady a jejich konvergence/divergence

#2 18. 10. 2020 14:28

Re: Nekonečné řady a jejich konvergence/divergence

#3 19. 10. 2020 16:58

Re: Nekonečné řady a jejich konvergence/divergence

Zápatí