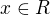Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 06. 2009 19:12
Prosím o pomoc
Omlouvám se že je to na edisku
http://www.edisk.cz/stahni/02561/img005.jpg_1.23MB.html
potřeboval bych pomoc s vypočítání 8 příkladů ve třetím cvičení. Děkuji
Offline
![$\sqrt[5]{4^x} = 4^{\frac{x}{5}}$](/mathtex/14/14cf929ed37828b735c568b9020993a6.gif "kopírovat do textarea")
OPRAVENO!!!
![$(\sqrt[3]{x\sqrt{x^2}})^2 = (\sqrt[3]{x.x})^2 =(\sqrt[3]{x^2})^2 = (x^{\frac{2}{3}})^2 = x^{\frac{4}{3}} $](/mathtex/d3/d3f4ad6e188b4dbab71925e220c451e9.gif "kopírovat do textarea")
![$\sqrt[3]{x\sqrt{x^2\sqrt{x}}} = x^{\frac{1}{3}} . x^{\frac{2}{2.3}} . x^{\frac{1}{2.2.3}} = x^{\frac{3}{4}} = \sqrt[4]{x^3}$](/mathtex/12/12d82dd7a03899dfbc36d754ec958019.gif "kopírovat do textarea")
![$\sqrt[3]{8^{x+1}}\cdot\sqrt{2^x}=2^{x+1}\cdot2^{\frac x2}=2^{\frac{3x}2+1}=2\sqrt{2^{3x}}$](/mathtex/bf/bfd3eba024323572894d2272982ea80c.gif "kopírovat do textarea")
pro 