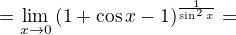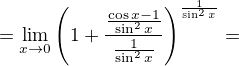Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita funkce - důkaz její neexistence (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 11. 2020 16:03
Limita funkce - důkaz její neexistence
Zdravím,
mám problém s jednou úlohou nevím v ní jak dál třeba by mi někdo dokázal poradit jakým způsobem pokračovat
Mám spočítat limitu nebo dokázat, že limita neexistuje.
\lim_{x\to0}(\cos x)^{\frac{1}{\sin^{2} x}}
z limity je jasné, že existovat nebude, už jen proto že po dosazení by mi ve zlomku vyšlo 1/0, ale nenapadá mě moc jak to dokázat matematicky. Možná snad pře Heineho větu, ale nevím kde se odpíchnout.
Offline
- (téma jako vyřešené označil(a) Proch)
#3 06. 11. 2020 16:11 — Editoval Ferdish (06. 11. 2020 16:12)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Limita funkce - důkaz její neexistence
Zlomok síce vyjde nekonečno, ale ten zlomok je v exponente - ak dosadíme za [mathjax]x=0[/mathjax] aj do kosínusu, tak dostaneme [mathjax]1^{\infty }[/mathjax], čo je neurčitý výraz.
Na základe vykreslenia danej funkcie do Desmosu vidíme, že funkcia je na okolí bodu [mathjax]x=0[/mathjax] spojitá, takže limita v nule bude existovať.
Offline
#5 08. 11. 2020 18:28
- AmayaYakushi

- Zelenáč
- Příspěvky: 5
- Reputace: 0
Re: Limita funkce - důkaz její neexistence
↑ surovec:
neni to spis postup, jak vypocitat limitu v +-nekonecnu? ,ale v zadani je pokud jde x k nule.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita funkce - důkaz její neexistence (TOTO TÉMA JE VYŘEŠENÉ)