Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Algebraické struktury (TOTO TÉMA JE VYŘEŠENÉ)
#2 21. 01. 2009 11:25 — Editoval Marian (21. 01. 2009 14:23)
Re: Algebraické struktury
↑ dubova:
Vypadá to jako okruh ke státnicím učitelství matematiky pro 2. stupeň ZŠ. Ale co já s tím, a co ostatní s tím? V pravidlech fóra je jasně napsáno, že se mají pokládat jasné explicitní dotazy. Myslím, že toto není tento případ.
Zkus to více rozvinout ...
Offline
#6 11. 06. 2009 22:10 — Editoval kaja(z_hajovny) (11. 06. 2009 22:13)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Algebraické struktury
Mozna ano, mozna ne, ale argumentuje spatne.
Pletete si -a jako prvek opacny k prvku a vzhledem k operaci plus v kolecku a -a jako cislo -1 krat a, tj prvek opacny vzhledem ke scitani
pokud -a oznacim opacny prvek vzhledem k operaci plus v kolecku tak musi platit
a+(-a)+a*(-a)=0
a odsud
(-a)= -a/(a+1)
kde -a napravo je "klasicky opacny prvek"
treba pro a=2 mame opacny prvek -a=-2/3
a zkuste si schvalne tou nasi operaci plus v kolecku secist 2 a -2/3, vyjde opravdu nula :)
problem s najitim inverzniho prvku vidim jenom pro a=-1.
Offline
#7 11. 06. 2009 22:26 — Editoval BrozekP (11. 06. 2009 22:27)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Algebraické struktury
Množina 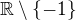 s tou operací bude tvořit grupu. Nebo se pletu?
s tou operací bude tvořit grupu. Nebo se pletu?
Offline
#8 11. 06. 2009 22:55 — Editoval kaja(z_hajovny) (11. 06. 2009 22:56)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Algebraické struktury
Asi ano, jeste je potreba ukazat, ze mnozina je vzhledem k teto operaci uzavrena, tj ze pokud a ani b nebudou -1, tak vysledek taky nebude -1. Snazil jsem se dukaz vmacknout na kraj lidovek (ktery je uz castecne popsany predeslymi vypocty) a vypada, ze to platit bude. ;)
Offline
#9 11. 06. 2009 23:21
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Algebraické struktury
Nechť 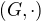 je multiplikativní grupa pod
je multiplikativní grupa pod  . Tedy například
. Tedy například ![kopírovat do textarea $\mathbb{Q}[\sqrt 2]\setminus\{0\}$](/mathtex/c3/c346116862930ca33b1456e6ce9ee164.gif) , {1}, nebo {1,-1}. Množina
, {1}, nebo {1,-1}. Množina 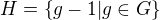 s operací
s operací 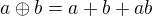 je grupou, protože
je grupou, protože 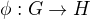 dané vztahem
dané vztahem 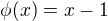 je grupovým izomorfizmem (bijekcí je zřejmě a skutečně je i homomorfizmem, neboť
je grupovým izomorfizmem (bijekcí je zřejmě a skutečně je i homomorfizmem, neboť 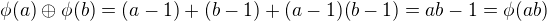 ).
).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#11 28. 04. 2010 17:42
Re: Algebraické struktury
↑ Djoszee:možná mohl, ale ne v tomto vyřešeném tématu, založ si vlastní a rovnou tam napiš, s čím máš problém.
Vesmír má čas.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Algebraické struktury (TOTO TÉMA JE VYŘEŠENÉ)
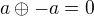 , teda
, teda 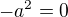 a to plati len pre
a to plati len pre  . Dakujem.
. Dakujem.