Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 12. 2020 16:46
Práce plyny
Ahoj, mam tento příklad:
1 mol kysliku expanduje z objemu 10l, t=25°C na konečný objem 50l při teplotě 100°C. Vypočítejte změnu tepla, vnitřní energie a objemovou práci. Přepokládejte idealní chování plynu a reverzibilní provedení. Cpm=27,18J/mol.K
nevím si rady, zda to mám počítat za konstantního tlaku (izobarický děj )nebo jako adiabatický děj.
Offline
#3 19. 12. 2020 19:14 — Editoval Mirek2 (19. 12. 2020 19:17)
- Mirek2
- Příspěvky: 1213
Re: Práce plyny
Podle zadání se teplota mění.
Jde použít Gay-Lussacův zákon pro izobarický děj?
Offline
#5 20. 12. 2020 00:27
Re: Práce plyny
Doufám, že se to počítá takto:
Element práce je
[mathjax]\delta A = pdV[/mathjax]
protože tlak je konstantní, tak platí i
[mathjax]\Delta A = p \Delta V[/mathjax]
Změna vnitřní energie by měla být
[mathjax]\Delta U = C_V \Delta T[/mathjax]
kde to Cv je tepelná kapacita při konstantním objemu. Já ovšem nevím, co je to to Cpm. Pokud je to tepelná kapacita za konstantního tlaku, tak se od toho bude muset ještě odečíst ta vykonaná práce.
A přijaté teplo se spočítá dle 1. TD zákona - ze změny vnitřní energie a vykonané práce. Zase - pokud je ta Cpm tepelná kapacita za konstantního tlaku, tak se to může počítat rovnou
[mathjax]\Delta Q = C_p \Delta T[/mathjax]
Offline
#6 20. 12. 2020 14:58 — Editoval Mirek2 (20. 12. 2020 15:02)
- Mirek2
- Příspěvky: 1213
Re: Práce plyny
Nešla by úloha řešit tak, že se děj rozdělí na a) izotermickou expanzi, b) izochorické zahřátí?
Cpm nejspíš bude molární tepelná kapacita při stálém tlaku.
Nezdá se mi, že by šlo o izobarický děj.
Offline
#7 20. 12. 2020 17:25
Re: Práce plyny
Já nevím. Pokud víme, že je to mol ideálního plynu, můžeme spočítat i ty tlaky, vlastně, protože
[mathjax]pV = nRT[/mathjax]
tedy
[mathjax]p = nRT/V[/mathjax]
Takže to s největší pravděpodobností izobarický děj nebude. A cesta určitě vede přes to složit to ze svou dějů, otázkou ovšem je z jakých.
Protože podle mě musíme využít toho, že známe tepelnou kapacitu při konstantním tlaku, takže jeden z těch dějů by měl být izobarický. Při něm zvedneme tu teplotu z 25°C na 100°C, a spočítáme kolik na to padlo tepla. Akorát úplně nevím, jak zjistit, jaká část tepla se změnila na vnitřní energii, a jaká na práci.
Druhý krok by mohl být izotermický děj - tam už se vnitřní energie nemění a všechno teplo se změní na práci.
Ale nějak se nemůžu zbavit pocitu, že pro tu první část budeme potřebovat znát i tu tepelnou kapacitu při konstantním objemu - tedy že budeme potřebovat znát tu konstantu [mathjax]\kappa[/mathjax] jež se vyskytuje při adiabatickém ději. A tu zadanou nemáme...(asi není problém si ji najít, otázka je, jestli to můžeme dělat).
Pokud bychom ji tedy vzali z tabulek, spočteme si [mathjax]C_{Vm}[/mathjax] - tedy tepelnou kapacitu při konstantním objemu, a potom (pro izobarický děj)
[mathjax]\Delta Q = C_{pm}\Delta T[/mathjax]
[mathjax]\Delta A = C_{Vm}\Delta T[/mathjax]
Ale když už budeme znát Cvm, tak můžeme udělat i to co navrhuješ ty, tedy zahřát to izochoricky, potom
[mathjax]\Delta Q = C_{Vm}\Delta T[/mathjax]
[mathjax]\Delta A = 0[/mathjax]
což je ještě jednodušší. A zbytek už je stejný. Jen mě pořád mate, že máme zadanou Cpm, a né Cvm,
Offline
#8 21. 12. 2020 12:47 — Editoval Mirek2 (23. 12. 2020 13:48)
- Mirek2
- Příspěvky: 1213
Re: Práce plyny
Lze provést přibližné aproximace, když děj rozdělíme na dva, např.
- izotermický (při teplotě T1) a izochorický (z teploty T1 na T2), nebo
- izobarický (z teploty T1 na teplotu T2) a izotermický (při teplotě T2)
a použijeme stavovou rovnici pro 1 mol: [mathjax]pV=RT[/mathjax].
První způsob:
a) izotermická expanze
stálá teplota, tudíž vnitřní energie se nemění, [mathjax]\Delta U = 0[/mathjax]
soustava přijme teplo [mathjax]Q_1[/mathjax] a vykoná práci [mathjax]W'[/mathjax]
[mathjax]Q_1=W'=RT_1\ln\frac{V_2}{V_1}= [/mathjax] (8,31 . 298 . 1,61) J = 3985 J
a) izochorické ohřátí
stálý objem, práce se nekoná
soustava přijme teplo [mathjax]Q_2[/mathjax] a zvýší vnitřní energii
[mathjax]Q_2=\Delta U =C_V \Delta T=(C_p-R)\Delta T =[/mathjax] (18,9 . 75) J = 1415 J
celkem
soustava přijala teplo [mathjax]Q=Q_1+Q_2 =[/mathjax] 5400 J
vnitřní energie se zvýšila o [mathjax]\Delta U =[/mathjax] 1415 J
soustava vykonala práci [mathjax]W' =[/mathjax] 3985 J
Offline
#10 22. 12. 2020 12:23 — Editoval Mirek2 (23. 12. 2020 13:49)
- Mirek2
- Příspěvky: 1213
Re: Práce plyny
↑ MichalAld:
Z pV-diagramu je vidět, že nebude stejná práce (plocha pod izotermou)
při ději izobarický + izotermický jako při ději izotermický + izochorický.
Stejná vychází jen vnitřní energie.
V tomto PDF na str. 48 se ve stejném příkladu počítá změna entropie. Nevím, jestli by to pomohlo.
https://ufch.vscht.cz/files/uzel/001386 … redirected
Offline
#11 22. 12. 2020 12:25
- Mirek2
- Příspěvky: 1213
Re: Práce plyny
↑ Jaja360:
Ahoj,
zkus dát tento příklad do sekce Fyzika, tam by se na to mohlo podívat víc očí.
Offline
#13 22. 12. 2020 13:41 — Editoval Mirek2 (22. 12. 2020 17:34)
- Mirek2
- Příspěvky: 1213
Re: Práce plyny
Ještě během odpoledne napíšu, proč si myslím, že to není ani izobarický ani adiabatický děj.
Aha - už to napsal ↑ MichalAld: níže.
Offline
#14 22. 12. 2020 17:13 — Editoval MichalAld (22. 12. 2020 17:15)
Re: Práce plyny
↑ Mirek2:
Zkusím to taky. Protože všechny děje by měly jít popsat jako
[mathjax]pV^k = const[/mathjax]
tedy
[mathjax]p_1V_1^k = p_2V_2^k[/mathjax]
a podle velikosti k lze poznat, o jaký děj jde (k=0 izobarický, k=1 izotermický, k= adiabatický a k=
adiabatický a k= izochorický).
izochorický).
Když za p dosadíme z rovnice ideálního plynu, a trochu si s tím pohrajeme, měli bychom dostat (nechce se mi to sem všechno psát) že
[mathjax]k=1-\frac{\ln\frac{T_1}{T_2}}{\ln \frac{V_1}{V_2}}[/mathjax]
Pro náš případ tedy (doufám, že to mám správně).
[mathjax]k=1-\frac{\ln\frac{273.15+25}{273.15+100}}{\ln \frac{10}{50}}=1-\frac{\ln 0.8}{\ln 0.2} = 1-0.1386 = 0.861[/mathjax]
Takže to není ani jeden z těch běžných dějů. Ono to bylo celkem jasné, když jsou zadané hezké teploty ve °C, že to nemůže vyjít hezky v Kelvinech.
Ale jinak je to vidět i bez počítání - izobarický by musel být konstantní poměr V/T, což na první pohled není ... (druhá teplota není 5x vyšší než ta první, není ani 2x vyšší).
A adiabatický děj to být nemůže, protože s rostoucím objemem by musela teplota klesat, a né růst.
Offline
#15 22. 12. 2020 17:20 — Editoval MichalAld (22. 12. 2020 17:22)
Re: Práce plyny
Mě by spíš zajímala jiná věc - jestli se dá nějak jednoduše ukázat, že vykonaná práce je vždy stejná, bez ohledu na to, jakým způsobem se do cílového stavu dostaneme.
Že bude vnitřní energie stejná, to je jasné - vnitřní energie je stavová veličina, ta na cestě nezávisí. Ale u práce, ani u tepla to podle mě nemusí být nutně pravda...
A teď koukám, že tys to vlastně psal, že to stejné nevychází.. tak to ani nemusím dokazovat.
Ona to vlastně záhada není, záhada by byla kdyby to stejně vycházelo. Takto je to jasné ... a úloha má tím pádem nekonečné množství řešení.
Prostě teplo, ani práce nejsou stavové veličiny (v rámci vyšší matematiky to znamená, že to nejsou úplné diferenciály) a tudíž jejich hodnoty obecně závisí na integrační cestě. Vnitřní energie (a třeba entropie) naproti tomu úplné integrály jsou - a jejich hodnota na integrační cestě nezávisí - závisí jen na koncových bodech.
Offline
#16 22. 12. 2020 17:33 — Editoval Mirek2 (22. 12. 2020 17:35)
- Mirek2
- Příspěvky: 1213
Re: Práce plyny
Přemýšlím, jestli by to nešlo nějak s pomocí entropie - takový příklad je na str. 48 zde (jinak stejné zadání), ale zatím mě nenapadlo, co s tím.
https://ufch.vscht.cz/files/uzel/001386 … redirected
Offline
#17 22. 12. 2020 17:49
Re: Práce plyny
No asi šlo, místo tepla můžeme doddávat entropii ... ale to stejně neřeší náš problém, pro každý způsob, jak plyn dostaneme do cílového stavu, bude vykonaná práce jiná. Entropii dodáme vždy stejnou - ale nebude to stejné množství tepla ... když dodáme entropii při vyšší teplotě, bude to více tepla, než když dodáme entropii při nižší teplotě.
V tomhle případě by bylo asi lepší to složit z izotermického a adiabatického děje - adiabatický děj zachovává entropii. Takže celý díl entropie předáme při izotermickém ději - a pak to adiabaticky stlačíme/roztáhneme abychom se dostali kam potřebujeme.
A taky to můžeme udělat mnoha způsoby - nejprve izotermický pak adiabatický, nebo naopak, nebo to střídat...
Pokud zůstaneme u těch dvou prvních variant - tj kombinace jednoho izotermického a jednoho adiabatického děje, tak je jasné, že když předaná entropie bude v obou případech stejná (musí být, je to stavová veličina) tak teplo nebude - protože jednou bude ten izotermický děj probíhat při nízké teplotě, podruhé při vysoké.
Což když o tom tak přemýšlím, tak je to vlastně Carnotův cyklus. A když si namísto p-V diagramu nakreslíme T-S diagram, tak to vše vypadá mnohem jednodušeji, protože jsou tam jen vodorovné a svislé čáry. Buď jdeme nejdřív vodorovně, nebo nejdřív svisle. Případně můžeme taky po schodech. Při vodorovném "pohybu" se předává entropie, při svislém né (vodorovný děj je izotermický, svislý adiabatický - také se říká izoentropický). Změna entropie je vždy stejná, ale dodané teplo né, protože (při izotermickém ději) je [mathjax]\Delta S = \Delta Q /T[/mathjax].
A práce odpovídá dodanému teplu mínus změna vnitřní energie - a změna vnitřní energie je také vždy stejná, nezávislá na cestě.
Offline
#18 22. 12. 2020 18:10 — Editoval MichalAld (22. 12. 2020 18:47)
Re: Práce plyny
Pro entropii (změnu entropie) ideálního plynu by měl platit vztah:
[mathjax]\Delta S = n [C_{Vm} \ln \frac{T_2}{T_1} + R \ln \frac{V_2}{V_1}][/mathjax]
To můžeme spočítat přímo ze zadaných hodnot. A potom se můžeme svobodně rozhodnout, při jaké teplotě tam tu entropii (teplo) dodáme, může to být cokoliv mezi T1 a T2, případně i kombinace. Z toho nám plyne minimální a maximální množství tepla, které může být při tomto ději dodáno - a to nám následně určuje kolik plyn může vykonat práce.
Ale je klidně možné, že lze vymyslet i jiné způsoby, jak se dostat do cílového stavu, a vykonat ještě více (či ještě méně) práce. Pokud bychom systém mohli i ochlazovat, tak to nejspíš žádné omezení nemá ...
Offline
#19 22. 12. 2020 20:01 — Editoval Mirek2 (22. 12. 2020 21:32) Příspěvek uživatele Mirek2 byl skryt uživatelem Mirek2. Důvod: Zrušeno
#20 23. 12. 2020 11:45 — Editoval Mirek2 (23. 12. 2020 13:51)
- Mirek2
- Příspěvky: 1213
Re: Práce plyny
↑ MichalAld:
Z polytropického děje můžeme vypočítat práci.
[mathjax]pV^k = {\rm konst}[/mathjax], ze stavové rovnice platí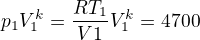
tedy [mathjax]pV^k = [/mathjax] 4 700 (jednotku nepotřebujeme),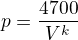
práce vykonaná plynem![kopírovat do textarea $W=\int_{V_1}^{V_2}p\,{\rm d}V=\int_{V_1}^{V_2}\frac{4700}{V^k}\,{\rm d}V=4700\[\frac{V^{1-k}}{1-k}\]_{V_1}^{V_2}=4540\,{\rm J}$](/mathtex/08/08bd9857663946581c77a517302125cd.gif)
Nevím ale, zda a jak lze vypočítat změnu vnitřní energie.
Konstanta [mathjax]k[/mathjax] = 0,861 je vypočtena výše.
Offline
#22 23. 12. 2020 11:56
Re: Práce plyny
Každopádně mi přijde, že problematika značně přesahuje obzor znalostí původní tazatelky...takže bych jí doporučil na uvedený problém upozornit a zeptat se, jak je to vlastně myšleno (že teplo a práce závisí na tom, jakým způsobem systém do cílového stavu dostaneme, a jaký způsob tedy máme zvolit).
Mě osobně přijde nejelegantnější systém adiabaticky ochladit až (téměř) na absolutní nulu, potom do něj nacpat potřebnou entropii - což odpovídá (téměř) nulovému teplu, a pak jej zase adiabaticky ohřát až do cílového stavu.
I bez počítání lze dospět k tomu, že systém nepřijme (téměř) žádné teplo, a zvýšení vnitřní energie bude pocházet (téměř) čistě z mechanické práce.
Offline
#23 23. 12. 2020 13:42
- Mirek2
- Příspěvky: 1213
Re: Práce plyny
↑ MichalAld:
Příklad je vyřešen, díky za spolupráci.
Doplním, že vnitřní energie ideálního plynu závisí jen na teplotě, nezávisí na způsobu, jakým se soustava do určitého stavu dostala.
Zadání rozumím tak, že plyn se postupně ohřívá z nižší teploty na vyšší (v průběhu děje nedojde k ochlazení), podobně objem se postupně zvyšuje.
Když vypočítám práci postupem dějů (izotermický + izochorický) a postupem dějů (izobarický + izotermický) a jejich průměr, vychází téměř stejná hodnota jako při polytropickém ději, což není překvapením.
Offline
#25 23. 12. 2020 14:05 — Editoval Mirek2 (24. 12. 2020 15:53)
- Mirek2
- Příspěvky: 1213
Re: Práce plyny
↑ Jaja360:
Ahoj,
konečně se zdá, že jsme příklad spojenými silami vyřešili - nejspíš to půjde ještě nějak přes entropii. Jestli to bylo poněkud nepřehledné, rád sestavím celé řešení do jednoho "okna". Díky za zajímavý příklad.
http://old.vscht.cz/fch/cz/pomucky/FCH4Bc.view.pdf
Offline
