Matematické Fórum

Jaja360 · 23. 12. 2020 20:23

↑↑ Mirek2:

Ahoj,

děkuji, ale mohla bych tě poprosit o celé řešení, ztrácím se v tom, a ráda bych měla ujasněno jak řešení mělo vypadat.

pietro · 28. 12. 2020 12:13

↑ Jaja360: dopĺňam obrázok ku výpočtu Mireka2

https://forum.matweb.cz/viewtopic.p … 58#p617558

https://ctrlv.sk/tjOB

Mirek2 · 28. 12. 2020 16:46 — Editoval Mirek2 (28. 12. 2020 16:58)

Shrnutí

Polytropický děj: [mathjax]p_1V_1^n= p_2V_2^n[/mathjax]

Ze stavové rovnice pro 1 mol [mathjax]pV=RT[/mathjax] vyjádříme [mathjax]p[/mathjax] a dosadíme do předchozí rovnice, dostaneme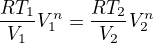

$\frac{RT_1}{V_1}V_1^n= \frac{RT_2}{V_2}V_2^n$

neboli

[mathjax] T_1 V_1^{n-1}= T_2 V_2^{n-1}[/mathjax]

logaritmujeme

[mathjax] \ln{T_1}+(n-1)\ln{V_1}= \ln{T_2}+(n-1)\ln{V_2}[/mathjax]

po úpravě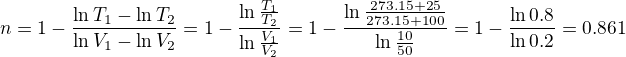

$n=1-\frac{\ln{T_1}-\ln{T_2}}{\ln{V_1}-\ln{V_2}}=1-\frac{\ln\frac{T_1}{T_2}}{\ln \frac{V_1}{V_2}}=1-\frac{\ln\frac{273.15+25}{273.15+100}}{\ln \frac{10}{50}}=1-\frac{\ln 0.8}{\ln 0.2} = 0.861$

Pak - konstanta [mathjax]R=[/mathjax] 8,314 J/(mol.K), jednotku nepotřebujeme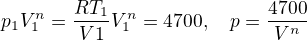

$p_1 V_1^n =\frac{RT_1}{V1} V_1^n=4700, \quad p =\frac{4700}{V^n}$

Plyn vykonal práci (v chemii se uvažuje objemová práce - zvážit, zda bude kladná, nebo záporná)

$W'=\int_{V_1}^{V_2}p\,{\rm d}V=\int_{V_1}^{V_2}\frac{4700}{V^n}\,{\rm d}V=4700\[\frac{V^{1-n}}{1-n}\]_{V_1}^{V_2}=4540\,{\rm J}$

Změna vnitřní energie (platí Mayerův vztah [mathjax]C_p - C_V = R[/mathjax])

[mathjax]\Delta U = C_{Vm}\Delta T=(C_{pm}-R)\Delta T=1415\,{\rm J}[/mathjax]

Plyn přijal teplo

[mathjax]Q=-\Delta U+W'=3125\,{\rm J}[/mathjax]

pietro · 29. 12. 2020 18:13

↑ Mirek2: Ahoj, posielam + za usilovnosť a komplexnosť. :-)

Matematické Fórum

#26 23. 12. 2020 20:23

Re: Práce plyny

#27 28. 12. 2020 12:13

Re: Práce plyny

#28 28. 12. 2020 16:46 — Editoval Mirek2 (28. 12. 2020 16:58)

Re: Práce plyny

#29 29. 12. 2020 18:13

Re: Práce plyny

Zápatí