Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 12. 2020 16:45
Součástky na spirále
Hraju si tady se skriptem v pythonu do Kicadu. Cílem je umístit součástky na spirálu tak, aby sousední byly stejně daleko od sebe.
Vyšel jsem ze skriptu, který je rozmístí na kružnici v konstantním úhlovém rozestupu. Přidal jsem nárůst poloměru. Jenže pak byly součástky čím dál řídčejší a to nechci. Tak jsem si řekl, že úhlový rozestup budu snižovat ve stejném poměru, jako roste poloměr. Kupodivu to ale vedlo ke značnému houstnutí a teda není mi moc jasné proč tak moc, čekal bych že to není moc vzdálená aproximace:-) Dal jsem tedy odmocninu z toho poměru a to už celkem sedí, i když rozestup zas mírně roste, ale to by asi nevadilo.
Takhle vypadá kód:
Code:
# spirala mm for refMin-refMax, fixed distance
def placeSpiralF(refText, refMin, refMax, angStart, angStep0, center, radStart, dr=0, component_offset=0, hide_ref=True, lock=False):
"""
Places components in a spiral/circle
refText: text of reference des.
refMin: min ref. des. number
refMax: max ref. des. number
angStart: Starting angle
angStep0: First step of angle in spiral
center: Tuple of (x, y) mm of spiral center
radStart: Starting radius of the spiral in mm
dr: radius change between components
component_offset: Offset in degrees for each component to add to angle
hide_ref: Hides the reference if true, leaves it be if None
lock: Locks the footprint if true
"""
pcb = GetBoard()
#deg_per_idx = angTotal / (refMax-refMin)
for idx in range(refMin, refMax+1):
rd = refText + str(idx)
part = pcb.FindModuleByReference(rd)
radius = (radStart + dr * idx)
angle = (angStart + idx * angStep0 / math.sqrt(radius/radStart)) % 360;
print "{0}: {1}, {2}".format(rd, angle, radius)
xm = center[0] + math.cos(math.radians(angle)) * radius
ym = center[1] + math.sin(math.radians(angle)) * radius
part.SetPosition(wxPoint(FromMM(xm), FromMM(ym)))
part.SetOrientation(angle * -10)
if hide_ref is not None:
part.Reference().SetVisible(not hide_ref)po použití placeSpiralF("D", 0, 71, 0.0, 25.0, (0, 0), 12.0, 0.33) je výsledek:
Zajímalo by mě, zda existuje nějaké jednoduché řešení, aby to vyšlo přesně, např. nějaká mocnina kousek pod 1/2, nebo to není tak jednoduché a mám se spokojit s tím jak to je:-)
Offline
#2 28. 12. 2020 17:51
Re: Součástky na spirále
Moc to nechápu, podle mě by mělo platit, že
[mathjax]dl = r d\varphi[/mathjax]
Takže pokud chceš mít konstantní L, tak by přírustek úhlu měl být L/r.
Problém je možná v tom, že ten úhel počítáš jako idx * angStep0 / korekce. Jenže ty bys měl počítat jen ten poslední přírustek úhlu, a předchozí úhel si pamatovat (protože ten byl vypočten z jiných radiusů, než co máš teď).
Offline
#3 28. 12. 2020 19:36
Re: Součástky na spirále
Vlastně je tam ještě druhý problém, že by to chtělo i konstantní stoupání.
Nejlepší by teda asi bylo, kdyby byly nějaký dvě řady, nebo funkce, kde by z nastavených parametrů a z indexu vznikl úhel a poloměr.
[mathjax]\varphi_i = f_1(\varphi_0, r_0, rozestup, stoupání, i)[/mathjax]
[mathjax]r_i = f_2(\varphi_0, r_0, rozestup, stoupání, i)[/mathjax]
Ale teda nenapadá mě, jak ty funkce vymyslet - kromě nějakého polynomu a pokus-omyl, což se mi nechce, vzhledem k tomu, že to nejspíš použiju jednou za x let na nějaký blikátko pro děti na kroužek.
Offline
#4 28. 12. 2020 20:41 — Editoval laszky (28. 12. 2020 23:24)
Re: Součástky na spirále
↑ edison:
Ahoj, pokud bych se mel podelit o svuj "navod", snazil bych se nejprve rozmistit body po spirale tak, aby mely od sebe stejnou vzdalenost.
Spirala:
[mathjax]r=a\phi[/mathjax]
Body:
[mathjax] x_i = r_i\cos\phi_i = a\phi_i\cos\phi_i[/mathjax]
[mathjax]y_i = r_i\sin\phi_i = a\phi_i\sin\phi_i[/mathjax]
Stejna vzdalenost:
[mathjax]L^2 = (x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2[/mathjax]
Po uprave:
[mathjax]\phi_{i+1}^2+\phi_i^2 - 2\phi_i\phi_{i+1}\cos(\phi_i-\phi_{i+1})=\frac{L^2}{a^2}[/mathjax]
Tato nelinearni rovnice ti da posloupnost uhlu [mathjax]\{\phi_i\}[/mathjax] pomoci kterych dopocitas [mathjax]r_i=a\phi_i[/mathjax].
EDIT:
Vysledek pak vypada napr. takto: https://ibb.co/dQGDYHp
Pokud navic vezmes v uvahu, ze normalovy smer spiraly je [mathjax](\sin\phi_i+\phi_i\cos\phi_i,\phi_i\sin\phi_i-\cos\phi_i),[/mathjax]
potom ziskas: https://ibb.co/MGqKQpY nebo dokonce https://ibb.co/j55FL0H
Offline
#6 29. 12. 2020 09:36
Re: Součástky na spirále
Tak díky oběma, nějak to dám dohromady.
Nakonec se mi zalíbila metoda, kdy generuju tu spirálu v přiměřeném rozlišení, např. 0,1 mm a vždy při překročení nastavené vzdálenosti od poslední pozice tam posadím součástku.
Když pak od středu budou jezdit rozsvícený úseky, bude to vypadat efektně. Ještě k tomu by to mělo vydávat haluzní zvuly:-) Druhá věc je, jestli budou ochotní připájet 96 LEDek a z druhý strany desky 12 posuvných registrů.
Offline
#7 30. 12. 2020 07:45
Re: Součástky na spirále
Kdyby to někdo taky potřeboval, tak tady:
Code:
# archimedova spirala, mm, refMin-refMax
def spiral(refText, refMin, refMax, angStart, center, rMin, stoup, dist, component_offset=0, hide_ref=True, lock=False):
# r = a + b*fi
a = rMin
b = stoup / 2 / math.pi
ang = angStart
angStep = 0.01/(a + b * math.sqrt(refMax-refMin))
pcb = GetBoard()
idx = refMin
prevX=-123456
prevY=-123456
for i in range(0, 1000000):
ang += angStep
r = a + b * ang
x = center[0] + r * math.cos(ang)
y = center[1] + r * math.sin(ang)
if prevX == -123456 and prevY == -123456 or sqrt((x-prevX)**2 + (y-prevY)**2) >= dist:
rd = refText + str(idx)
part = pcb.FindModuleByReference(rd)
part.SetPosition(wxPoint(FromMM(x), FromMM(y)))
part.SetOrientation((math.degrees(ang) % 360) * -10)
prevX=x
prevY=y
idx+=1
if idx>refMax:
print "hotovo, otacek: " + str(ang/2/math.pi) + ", krok: " + str(math.degrees(angStep)/360.0) \
+ " deg = " + str(angStep * 2 * math.pi * r) + " mm na konci"
break
if i>=1000000:
print "Chyba: Mimo rozsah uhloveho indexu"A takhle zatím vypadá výsledek: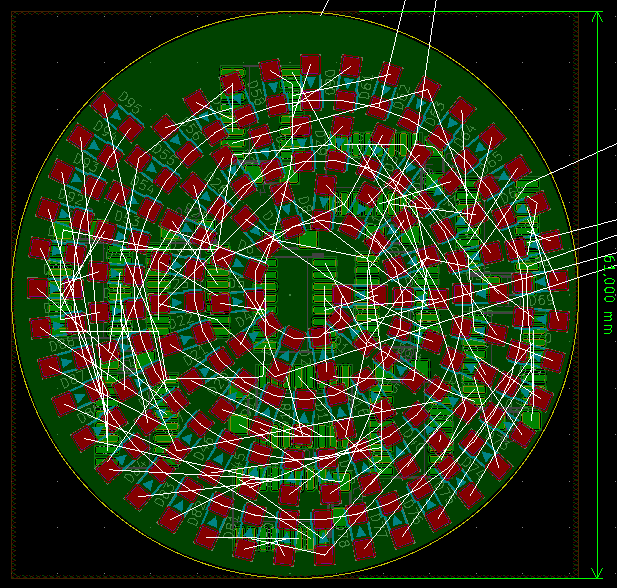
Teď už jen naroutovat spoje:-)
Offline
