Matematické Fórum

2M70 · 28. 12. 2020 21:43

Zadaná je funkce

$f(x)=ax,x\in (-\pi ,0)$
$f(x)=bx,x\in (0,\pi )$

kterou mám rozvést ve Fourierovu řadu.

Výsledek je tento "hnusný" složitý výraz:

$\frac{(b-a)\pi }{4}-\frac{2(b-a)}{\pi }\sum_{n=0}^{\infty }\frac{\cos (2n+1).x}{2n+1}+(a+b)\sum_{n=1}^{\infty }(-1)^{n+1}\frac{sin(nx)}{n}$

Bohužel nevím, jak se z tak jednoduché funkce dostane takový komplikovaný výraz.

Vím jenom základní vztahy pro výpočet koeficientů Fourierovy řady:

$f=\frac{a_{0}}{2}+\sum_{k=1}^{\infty }(a_{k}\cos \frac{2k\pi }{l}x+b_{k}\sin \frac{2k\pi }{l}x$

$a_{0}=\frac{2}{l}\int_{a}^{a+l}f(x)dx$

$a_{k}=\frac{2}{l}\int_{a}^{a+l}f(x)\cos \frac{2k\pi }{l}xdx$

$b_{k}=\frac{2}{l}\int_{a}^{a+l}f(x)\sin \frac{2k\pi }{l}xdx$

Dokáže někdo poradit?

jarrro · 29. 12. 2020 06:54

V tomto prípade je
$a_{k}=\frac{1}{\pi}\left(a\int\limits_{-\pi}^{0}{x\cos{\left(kx\right)}\mathrm{d}x}+b\int\limits_{0}^{\pi}{x\cos{\left(kx\right)}\mathrm{d}x}\right)$ a
$b_{k}=\frac{1}{\pi}\left(a\int\limits_{-\pi}^{0}{x\sin{\left(kx\right)}\mathrm{d}x}+b\int\limits_{0}^{\pi}{x\sin{\left(kx\right)}\mathrm{d}x}\right)$

2M70 · 29. 12. 2020 20:27

↑ jarrro:

Skoro to vyšlo, akorát první řada mi vychází

$\sum_{}^{}\frac{(\cos (n\pi )-1)\cdot (\cos (nx)}{n^{2}}$

a nevychází mi ta dvojka ve členu před touto řadou.

jarrro · 30. 12. 2020 00:22

$\cos{\left(n\pi\right)}-1$ je pre párne n nulové a pre nepárne n je to [mathjax]-2[/mathjax]

2M70 · 30. 12. 2020 09:52

↑ jarrro:

Dobře, ale tím stále nemám vyřešeno, jak dojdu k řadě

$\sum_{n=0}^{\infty }\frac{\cos (2n+1)x}{2n+1}$

jarrro · 30. 12. 2020 18:26

$a_{k}=\frac{1}{\pi}\left(a\int\limits_{-\pi}^{0}{x\cos{\left(kx\right)}\mathrm{d}x}+b\int\limits_{0}^{\pi}{x\cos{\left(kx\right)}\mathrm{d}x}\right)=\nl =\frac{1}{k^2\pi}\left(a\int\limits^{0}_{-\color{red}k\color{black}\pi}{x\cos{\left(x\right)}\mathrm{d}x}+b\int\limits_{0}^{\color{red}k\color{black}\pi}{x\cos{\left(x\right)}\mathrm{d}x}\right)$

2M70 · 30. 12. 2020 18:55

↑ jarrro:

Omlouvám se, ale teď jsem nepochopil tu změnu mezí - integruji per partes

jarrro · 31. 12. 2020 06:41

x=t/k
aby tam bolo iba [mathjax]x\cos{\left(x\right)}[/mathjax] resp. [mathjax]t\cos{\left(t\right)}[/mathjax], ale je jedno ako sa nazve premenná

2M70 · 02. 01. 2021 15:31

Ten příklad má ještě další pod-úkol:

Rozšiřte funkci f na celé R tak, aby se tvar její Fourierovy řady nezměnil.

Tady opravdu nevím :-(

jarrro · 02. 01. 2021 21:47

periodicky

2M70 · 02. 01. 2021 22:09

↑ jarrro:

Pro to rozšíření z (-pi, pi) na R budu potřebovat měnit ten Fourierův rozvoj, nebo nějak zdůvodnit/dokázat tu periodicitu?

jarrro · 02. 01. 2021 22:17

Každý fourrierov rozvoj má periódu [mathjax]l[/mathjax] (niektoré nie nutne najmenšiu)

2M70 · 02. 01. 2021 22:31

↑ jarrro:

Stačí tedy konstatovat, že Fourierova řada má nejmenší perodu 2 pi (od -pi do pi) a lze tedy 2 pi-periodicky rozšířit na celé R?

jarrro · 03. 01. 2021 08:32

↑ 2M70:áno

2M70 · 03. 01. 2021 08:34

↑ jarrro:

Může mi projít toto: ?

Periodické rozšíření fce f

Stačí znát periodickou fci v intervalu (0,T) a známe již funkci na celém R.
-> Periodickou fci s periodou T > 0 lze vytvořit z fce dané v intervalu (0,T).
Platí totiž: je-li 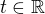$t\in \mathbb{R}$ , kT < T < (k+1) T, $k\in \mathbb{Z}$ ,
pak f(t) = f (t-kt), $t-kt\in (0,T)$ .
Takto vytvořená fce = periodické prodloužení fce f dané v intervalu (0,T).

Asi by to chtělo ty intervaly (0,T) nahradit (-pi, pi).

jarrro · 03. 01. 2021 08:48

áno ak predpokladám, že si chcel napísať $f{\left(t\right)}=f{\left(t-kT\right)}, t-kT\in (0,T)$

Matematické Fórum

#1 28. 12. 2020 21:43

Fourierova řada - složitý výsledek

#2 29. 12. 2020 06:54

Re: Fourierova řada - složitý výsledek

#3 29. 12. 2020 20:27

Re: Fourierova řada - složitý výsledek

#4 30. 12. 2020 00:22

Re: Fourierova řada - složitý výsledek

#5 30. 12. 2020 09:52

Re: Fourierova řada - složitý výsledek

#6 30. 12. 2020 18:26

Re: Fourierova řada - složitý výsledek

#7 30. 12. 2020 18:55

Re: Fourierova řada - složitý výsledek

#8 31. 12. 2020 06:41

Re: Fourierova řada - složitý výsledek

#9 02. 01. 2021 15:31

Re: Fourierova řada - složitý výsledek

#10 02. 01. 2021 21:47

Re: Fourierova řada - složitý výsledek

#11 02. 01. 2021 22:09

Re: Fourierova řada - složitý výsledek

#12 02. 01. 2021 22:17

Re: Fourierova řada - složitý výsledek

#13 02. 01. 2021 22:31

Re: Fourierova řada - složitý výsledek

#14 03. 01. 2021 08:32

Re: Fourierova řada - složitý výsledek

#15 03. 01. 2021 08:34

Re: Fourierova řada - složitý výsledek

#16 03. 01. 2021 08:48

Re: Fourierova řada - složitý výsledek

Zápatí