Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 12. 2020 21:18
Anulování koeficientů Fourierovy řady
Mám funkci f,  .
.
Mám určit, které koeficienty Fourierova rozvoje se anulují, pokud platí a
a  .
.
Vím, že se mají anulovat členy 
ale nevím, jak to dokázat.
Dále mám určit, jak se prodlouží funkce 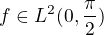 , na interval
, na interval  , aby její Fourierova řada měla tvar
, aby její Fourierova řada měla tvar 
Vím, že se sem takto formulované příspěvky nemají vkládat, ale tady opravdu nevím, jak na to.
Offline
#4 02. 01. 2021 21:54 — Editoval jarrro (02. 01. 2021 21:55)
Re: Anulování koeficientů Fourierovy řady
Veď si zistil, že [mathjax]f{\left(-x\right)}=f{\left(x\right)}[/mathjax] a
[mathjax]f{\left(x+\pi\right)}=-f{\left(x\right)}[/mathjax]a to je predsa rozširenie
MATH IS THE BEST!!!
Offline
#7 02. 01. 2021 22:48
Re: Anulování koeficientů Fourierovy řady
Protože v první části příkladu byla  , ale tady mám
, ale tady mám 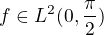 a na
a na  ji mám prodloužit.
ji mám prodloužit.
Když vezmu obecný vztqh pro Fourierův rozvoj
l...perioda
a porovnám s tímto příkladem
Vychází  ,
,  a kosinová řada s periodou
a kosinová řada s periodou 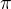 .
.
Kdybych uvažoval ty dvě podmínky, tak implikuje sudost
implikuje sudost má znamenat tzv. "antiperiodicitu"
má znamenat tzv. "antiperiodicitu"
Offline
#8 03. 01. 2021 08:41
Re: Anulování koeficientů Fourierovy řady
Veď si zistil, že pre [mathjax]\left(-\pi,\pi\right)[/mathjax]majú funkcie s tými vlastnosťami požadovaný tvar rozvoja, teda keď funkciu z [mathjax]\left(0, \frac{\pi}{2}\right)[/mathjax] rozšíriš na [mathjax]\left(-\pi,\pi\right)[/mathjax] tak, aby mala tie vlastnosti, tak bude mať rozvoj ti vlastnosti. Rozvoju je jedno či funkcia je na[mathjax]\left(-\pi,\pi\right)[/mathjax] jedinečná alebo vznikla rozšírením z kratšieho intervalu. Teda ak mi niečo neuniká.
MATH IS THE BEST!!!
Offline
