Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 06. 2009 15:19 — Editoval PitBull~--! (04. 06. 2009 15:19)
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
kombinatorika
mam tady 2 priklady a potreboval bych stim trochu pomoc
prvni priklad zni: je dano 0,2,4,6 kolik vznikne ctyrcifernych cislo s opakovanim a bez opakovani?
myslim ze je to variace ale nejsem si jisty
takze kdyz je to s opakovani tak to bude asi takhle P(4) - P(3) = 24 - 6 = 18
bez opakovani : 4^4 -3^3 ?
druhej priklad.
zadani zni student mel 10 otazek z toho 2 otazky zkousi, 3 neumi z 10 otazek. Jaka je pravdepodobnost ze dostane ty 2 co umi?
a ted uz vubec nevim co a jak.
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#2 04. 06. 2009 15:25
Re: kombinatorika
1)
Pokud to správně vnímám, tak na prvním místě nesmí být 0, pak už jo.
Takže bez opakování. Na první pozici máme 3 možnosti, na druhou také 3, na třetí 2 a na poslední 1. Výsledek je 3*3*2*1=18.
S opakováním. Na první pozici máme 3 možnosti, pak 4, 4 ,4. Výsledek je 3*4*4*4=192.
2)
Počet všech možností, jaké otázky může dostat je kombinace 2 prvků z 10, těch je 45.
Počet kombinací, ve kterých jsou 2 otázky, které student umí: Umí 7 otázek a libovolné 2 z nich chce dostat. Takže kombinace 2 prvků ze 7, těch je 21.
Pak 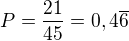
oo^0 = 1
Offline
#3 04. 06. 2009 15:59
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: kombinatorika
ten prvni priklad s opakovanim sem moc nepochopil muzes mi to vysvetlit podrobneji?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#4 04. 06. 2009 16:53 — Editoval docasne123 (04. 06. 2009 16:59)
- docasne123
- Příspěvky: 56
- Reputace: 0
Re: kombinatorika
ad. 1. příklad s opakováním. Jsou to variace určitě, protože záleží na pořadí tzn. číslo 2460 není to samé jako 6240.
Máš číslice 0;2;4;6. Číslo ale nezačíná 0 (nulou) 045 = 45. Takže podle pravidla součinu (myslím, že se to tak nazývá) si to můžeš říct takhle:
Ve čtyřcirferneém číslo _ _ _ _ mohou být na první pozici 3 číslice, a to: 2;4;6. Na druhé pozici už mohou být jakákékoliv ze čtyř číslic - i "0" (protože např. číslo 2046 je "normální") a může tam být znovu i číslo které bylo na první pozici (protože se jedná o variace s opakováním). Takže krát "4", stejně tomu je i u 3. i 4. pozice čtyčciferného čísla a proto:
Samozřejmě to lze vypočítat i přes variace s opakováním V´(4;4) * (3/4) tzn. 4. třída (jedná se o čtyřciferné číslo) ze čtyř prvků (máš na výběr z číslic 0;2;4;6) = 4^4 * (3/4) = 256 * (3/4) = 192
Ten zlomek 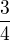 vyjadřuje, že to nemůže začínat 0 a proto bereš jakoby 3/4 z celého výsledku. 1/4 Možností by začínalo 0.
vyjadřuje, že to nemůže začínat 0 a proto bereš jakoby 3/4 z celého výsledku. 1/4 Možností by začínalo 0.
EDT: radši jsem to přepsal do Tex(u)
Offline
#5 04. 06. 2009 21:45
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: kombinatorika
a ten 2 priklad jeste prosim
kdyz student umi jenom 3 otazky a 7 neumi tak P = C(2,3)/C2,10) ?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#7 12. 06. 2009 20:52
Re: kombinatorika
Na poličce chceme rozestavit tři bílé, dva modré a dva červené hrnky.Kolika způsobyto lze provést: a)mají-li být hrnečky stejné barvy vedle sebe
b)mají-li být hrnečky stejné barvy vedle sebea modré mají být vlevo od červených??? Prosím , poraďte,,díky
Offline
#8 12. 06. 2009 21:02 — Editoval marnes (12. 06. 2009 21:06)
- marnes

- Příspěvky: 11227
Re: kombinatorika
↑ romule:
a) jsou tři barvy a máme je poskládat - permutace- 3! pokud nejde hrnečky jedné barvy rozlišit
b) MČB
MBČ
BMČ 3x
a´) pokud jde hrnky jedné barvy rozlišit, tak 3!3!2!2!
3! rozházení barev
3! jednotlivé možnosti pro bílou
2! modrou
2! červenou
Jo. A na začátku vás zdravím.
Offline