Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)
#1 06. 01. 2021 17:30
Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)
Zdravím,
potřebovala bych poradit s větou: Grupa, která má všechny vlastní podgrupy cyklické, je komutativní.
Máme ji vyvrátit / dokázat.
Mám tvrzení, že každá podgrupa cyklické grupy je cyklická a vím, že tvrzení nelze obrátit, neboli: grupa, která má všechny podgrupy cyklické, nemusí být cyklická (např. Prüferova grupa). Vím, že každá cyklická grupa je komutativní. Ovšem v zadané větě nemůžu nahradit komutativní grupu za cyklickou, že?
Offline
#2 07. 01. 2021 10:55
Re: Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)
Ahoj ↑ denvan:,
Co mozes povedat o grupe 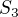 ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 07. 01. 2021 14:44 — Editoval denvan (07. 01. 2021 15:54)
Re: Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)
↑ vanok:
Tak grupa [mathjax]S_{3}[/mathjax] je izomorfní s [mathjax]S(\triangle )[/mathjax] (symetrie rovnostranného trojúhelníku). Jejími prvky tak jsou: identita, rotace+, rotace-, a 3 osové soum.
Má tedy řád 6, prvky mají řády: 1, 3, 3, 2, 2, 2.
Nejedná se o cyklickou grupu, podgrupy jsou: [mathjax]\{id\}[/mathjax] řádu 1, [mathjax]\langle Sa \rangle , \langle Sb \rangle , \langle Sc \rangle [/mathjax] řádu 2, [mathjax]\langle r+\rangle = \langle r-\rangle[/mathjax] řádu 3 a samotná [mathjax]S(\triangle )[/mathjax] řádu 6.
Offline
#4 07. 01. 2021 19:02
Re: Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)
↑ denvan:,
Poznamka:
Mohla si konstatovat, ze 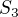 ma 6 prvkov, jej vlastne podgrupy ktore su cyklicke.
ma 6 prvkov, jej vlastne podgrupy ktore su cyklicke.
Ale ona sama nie je ani cyklicka a ani komutativna.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 07. 01. 2021 20:40
Re: Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)
↑ vanok:
Jasně, díky. Hledala jsem složitosti tam, kde nejsou.
Ještě bych se rovnou zeptala na jednu věc (pokud neobtěžuji), ať v tom mám trochu jasněji. Tvrzení: Grupa je komutativní právě tehdy, když všechny její vlastní podgrupy jsou komutativní.
Implikace zleva doprava je podle mého pravdivá, pokud komutativita platí pro všechny prvky mn. G, platí i pro její podmnožiny. Ale zprava doleva si nevím rady. Podle mého to neplatí, když jsou prvky komutativní v nějaké podgrupě a jiné prvky v další podgrupě také, nemusí to znamenat, že jsou navzájem komutativní i v dané grupě, ne?
Offline
#6 07. 01. 2021 22:02
Re: Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)
↑ denvan:,
Vsak aj na to ti dava odpoved aj ten priklad co som ti dal vyssie.
A dokazes najst aj ine priklady takych situacii?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 07. 01. 2021 22:40
Re: Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)
↑ denvan:,
Pridam ti tu dalsiu grupu, ktora nie je komutativna ( a tak pochopitelne nie je cyklicka) a ktorej podgrupy su cyklicke. Ide o  dihedralnu grupe, kde n je neparne.
dihedralnu grupe, kde n je neparne.
A tiez ti pripomeniem, ze mame aj priklad kde podgrupy su cyklicke a grupa i ked nie cyklicka moze byt komutativna: mozes mysliet na  , kde p je prvocislo.
, kde p je prvocislo.
No mame este plno dalsich prikladov .... no urcite to uvidis na prednaskach.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 08. 01. 2021 10:10
Re: Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)
↑ vanok:
Jasně, moc děkuji za tvé odpovědi.
Já se na to vždy snažím přijít nějak obecně, přitom stačí najít jeden konkrétní příklad a tím to vyvrátit. Díky :)
Na přednáškách to bohužel asi neuslyším, vyučující jede spíše styl „nauč se sám", což mi úplně nevyhovuje. Projede pár definic, vět a tím končí. K nějakým konkrétním příkladům se moc nedostane.
Offline
#9 08. 01. 2021 22:08 — Editoval vanok (08. 01. 2021 22:18)
Re: Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)
Ahoj ↑ denvan:,
Mozem ti pridat dalsiu grupu na premyslanie grupa kvaternionov ( ma 8 prvkov [mathjax]\pm 1,\pm i, \pm j,\pm k[/mathjax] )
grupa kvaternionov ( ma 8 prvkov [mathjax]\pm 1,\pm i, \pm j,\pm k[/mathjax] )
jej vlastne podgrupy su tieto 4 cyklicke groupy: [mathjax]<-1>, <i>, < j>,<k>[/mathjax] a ako iste dobre vies tato grupa nie je komutativna.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Grupy, podgrupy (G, která má všechny vl. podgr. cyklické, je komutat.)

