Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Komplexní křivkový integrál, obcházení singularity
#1 20. 03. 2021 17:22
Komplexní křivkový integrál, obcházení singularity
Souvisí s diskuzí v sousedním tématu:
Mám stejnou funkci,
Ale tentokrát jde o „obcházení“ singularity „malou kružnicí“, konkrétně bod  .
.
kde malá kružnice jde od 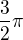 do
do 
Volím postup
Po dosazení
Po roznásobení
Po úpravách

Integrál je tedy
Provedeme limitu  , podle Lebesgueovy věty vsuneme do integrálu, integrand bude
, podle Lebesgueovy věty vsuneme do integrálu, integrand bude
Po dosazení![kopírovat do textarea $\int_{\frac{3}{2}\pi }^{-\frac{\pi }{2}}\frac{i}{3}\cdot exp(-i\frac{\pi }{3})d\varphi =\frac{i}{3}\cdot exp(-i\frac{\pi }{3})[-\frac{\pi }{2}-\frac{3}{2}]=$](/mathtex/9b/9b07d1d362a1d73c5c346103fb239077.gif)

Což je dost podivný výsledek...
Offline
#2 21. 03. 2021 14:39
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1060
- Reputace: 18
- Web
Re: Komplexní křivkový integrál, obcházení singularity
Přes jakou křivku se má počítat?
Offline
#3 21. 03. 2021 14:54
Re: Komplexní křivkový integrál, obcházení singularity
↑ Richard Tuček:
Celá integrovaná oblast je uzavřená křivkami
1) úsečka z = t, t jde od 0 do R
2) oblouk "velké kružnice" s průměrem R a od úhlu 0° do úhlu 2pi/3
3) úsečka z = t . exp (i . 2pi/3), tedy průvodič z počátku k průsečíku s "velkou kružnicí", úsečka (průvodič) svírá s kladnou poloosou úhel 2pi/3
ale to myslim nemá moc vliv na to, že:
uvnitř oblasti je bod - singularita exp(i. pi/3), a tu je pro spočtení integrálu potřeba obkroužit - je to "odskok" z úsečky (1) z = t k singularitě, ta se "obkrouží" "malou kružnicí" a zase návrat zpět na úsečku (1) z = t.
"Tunýlky" - spojnice úsečky (1) z = t s "malou kružnicí" - se "požerou", zůstane tedy integrál přes "malou kružnici", která je dána parametrizací  , kde krajní body kružnice jsou od
, kde krajní body kružnice jsou od 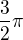 do
do  .
.
Offline
#4 21. 03. 2021 16:02 — Editoval Richard Tuček (21. 03. 2021 16:37)
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1060
- Reputace: 18
- Web
Re: Komplexní křivkový integrál, obcházení singularity
Integrál bych rozdělil na 3 křivkové
parametrizace:
1) fí(t)=t t od 0 do R
2) fí(t)=R*exp(it) t od 0 do (2/3)*pi
3) fi(t)=(R-t)*exp((2/3)*i*pi) t od 0 do R
Křivka mine singularitu exp((1/3)*i*pi)=(1/2)+i*odm(3)/2
Při výpočtu integrálu je nutno dosadit za z=fí(t), za dz=derivace fí(t) dt
Pro kontrolu můžeme zkusit reziduovou větu.
Křivkový integrál je 2*i*pi* rez v exp((1/3)*i*pi)
Křivka je kladně orientovaná a ve vnitřku je jedna singularita (pól násobnosti 1).
viz též můj web: www.tucekweb.info (analýza v komplexním oboru)
Offline
#5 21. 03. 2021 16:25
Re: Komplexní křivkový integrál, obcházení singularity
Richard Tuček napsal(a):
Integrál bych rozdělil na 3 křivkové
parametrizace:
1) fí(t)=t t od 0 do R
2) fí(t)=exp(it) t od 0 do (2/3)*pi
3) fi(t)=(R-t)*exp((2/3)*i*pi) t od 0 do R
Parametrizaci mám zadanou:
1) stejně
2) f (t) = R. exp(it), t od 0 do (2/3)*pi, pro R velké lze použít odhad a integrál přes tuto "velkou kružnici" je = 0
3) zadáno skoro stejně, f(t) = t * exp(i*fi), fi [0, 2/3 pi], t jde od R do 0.
Richard Tuček napsal(a):
Při výpočtu integrálu je nutno dosadit za z=fí(t), za dz=derivace fí(t) dt
To jsem ale již, předpokládám, udělal:

a

A teď jde podle mě o to, vypočítat integrál
což nevím moc jak, leda že bych použil ten přechod k limitě a zintegroval.
Offline
#6 21. 03. 2021 16:46
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1060
- Reputace: 18
- Web
Re: Komplexní křivkový integrál, obcházení singularity
pardon, spletl jsem se, má být 2) R*exp(it)
Tak ty integrály
1) integrál od 0 do R z funkce t/((t^3)+1) dt
2) integrál od 0 do (2/3)*pi z funkce (R*exp(it)/((R^3 * exp(3it)) +1)) * Ri*exp(it)
3) minus integrál od 0 do R z funkce (t*exp(2/3)ipi)/(t^3*exp((2/3)ipi*3) + 1)* exp(2/3)ipi)
Offline
#7 21. 03. 2021 16:54
Re: Komplexní křivkový integrál, obcházení singularity
Richard Tuček napsal(a):
pardon, spletl jsem se, má být 2) R*exp(it)
Tak ty integrály
1) integrál od 0 do R z funkce t/((t^3)+1) dt
2) integrál od 0 do (2/3)*pi z funkce (R*exp(it)/((R^3 * exp(3it)) +1)) * Ri*exp(it)
3) minus integrál od 0 do R z funkce (t*exp(2/3)ipi)/(t^3*exp((2/3)ipi*3) + 1)* exp(2/3)ipi)
Integrál přes tu křivku (3) mi vyšel stejný jako přes křivku (1), akorát přenásobený exp(2/3 * pi * i), což je v souladu se zadáním - integrály mají být shodné až na multiplikativní konstantu.
Offline
#8 22. 03. 2021 14:51
Re: Komplexní křivkový integrál, obcházení singularity
Tak mám správné dílčí výslledky -
2) Integrál přes "velkou kružnici" = 0
1+3):
(Integrál přes 

Obkroužení singularity:
Integrál (pro epsilon jde k nule):
Ale teď jde o to, jak z toho, s pomocí Cauchyovy věty, dostat finální výsledek,
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Komplexní křivkový integrál, obcházení singularity