Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 04. 2021 10:56
velikost výšky Va v trojúhelníku
Zdravím všechny. Mám zadány tři body trojúhelníku A=[4,-2], B=[2,6], C=[-2,0]. Vypočítal jsem směrový vektor BC s=(-4,-6), ten jsem převedl na normálový vektor n=(3,-2). Vytvořil jsem obecnou rovnici strany BC s výsledkem 3x-2y-16=0. Dále jsem si našel vzorec pro velikost vzdálenosti přímky od bodu. Když jsem tam dosadil hodnoty, tak mi vyšla nula. Zkuste mi poradit kde jsem udělal chybu.
Děkuji
Offline
- (téma jako vyřešené označil(a) mulder)
#3 05. 04. 2021 12:10 — Editoval Cheop (05. 04. 2021 12:45)
- Cheop
- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: velikost výšky Va v trojúhelníku
↑ mulder:
Do rovnice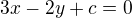 
musíš dosadit souřadnice bodu B nebo C a nikoliv bodu A.
Souřadnice bodu A dosazuješ až do vzorce pro vzdálenost bodu od přímky.
Nikdo není dokonalý
Offline
#5 05. 04. 2021 16:45
Re: velikost výšky Va v trojúhelníku
↑ mulder:vim, ze bych mel zalozit nove tema, ale ma se jeste vypocitat velikost uhlu ABC. Jen pro kontrolu zda to mam spravne, vyslo mi 132°16'. Pak se ma jeste vypocitat obvod. Tak jsem si vypocital velikosti vektoru stran a obvod mi vysel 21,78
Offline