Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrovateľnosť f(x) na intervale (TOTO TÉMA JE VYŘEŠENÉ)
#2 02. 04. 2021 17:38
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Integrovateľnosť f(x) na intervale
Zdravím,
predpokladám, že sa jedná o Riemannovskú integrovateľnosť resp. overovanie platnosti podmienok Riemannovskej integrovateľnosti. Čo o tom vieš resp. čo ste si o tom preberali?
Offline
#3 02. 04. 2021 17:59
Re: Integrovateľnosť f(x) na intervale
↑ Ferdish:
Áno, viem že ohraničená funkcia je riemannovsky integrovateľná ak spĺňa niektorú z nasledujúcich podmienok:
a) f(x) je spojitá
b) monožina nespojitosti funkcie má Jordamovu mieru nula;
c) f(x) je monotónna
Je mi zrejmé, že časti b), c) neplatia. Že neplatí časť a) vidím len z grafu, ale to zatiaľ nemôžem dokazať.
Offline
#4 02. 04. 2021 20:00 — Editoval Ferdish (02. 04. 2021 20:01)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Integrovateľnosť f(x) na intervale
Je to už dávno čo som mal prednášky z analýzy, ale ak sa nemýlim, tak funkcia je spojitá na nejakom intervale [mathjax]I[/mathjax] ak je spojitá v každom bode tohto intervalu. Ak funkcia nie je v niektorom bode definovaná, nie je v tomto bode spojitá. Z vyšetrenia definičného oboru by malo byť zrejmé, či funkcia je definovaná na celom uvažovanom intervale [mathjax]\langle0;8\rangle[/mathjax] alebo nie a to by malo riešiť aj otázku spojitosti na intervale [mathjax]\langle0;8\rangle[/mathjax].
Offline
#5 02. 04. 2021 20:41
Re: Integrovateľnosť f(x) na intervale
↑ Ferdish:
Ako nájsť tento definičný obor, pretože vychádza mi niečo naozaj škaredé a neviem čo s tým robiť?
Offline
#6 02. 04. 2021 20:57 — Editoval Ferdish (02. 04. 2021 21:31)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Integrovateľnosť f(x) na intervale
↑ Kart:
Možno by sa dalo využiť to, že vo výraze pod odmocninou máme 6 sínusov ale len 5 kosínusov, tým pádom v rámci výrazu máme funkciu [mathjax]f(x)=5(\sin x+\cos x)[/mathjax] a vzhľadom na nadbytočný sínus môžeme využiť vzťah [mathjax]\sin x+\cos x=\sqrt{2}\sin (x+\frac{\pi }{4})[/mathjax].
Offline
#7 02. 04. 2021 21:36
Re: Integrovateľnosť f(x) na intervale
↑ Ferdish:
Upravil som ten vyraz takto  a využil som vzorec
a využil som vzorec 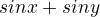 , ale stále mi to nevychádza. Nemôžem to správne upraviť.
, ale stále mi to nevychádza. Nemôžem to správne upraviť.
Offline
#8 02. 04. 2021 21:44
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Integrovateľnosť f(x) na intervale
Tak potom mi napadá ešte toto: https://www.mathcentre.ac.uk/resources/ … 2009-1.pdf
Offline
#10 03. 04. 2021 10:34
Re: Integrovateľnosť f(x) na intervale
↑ Ferdish:
Vďaka tomu som vyriešil príklad, díky moc, naozaj užitočné info
Offline
#11 03. 04. 2021 10:41 — Editoval Ferdish (03. 04. 2021 10:42)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Integrovateľnosť f(x) na intervale
↑ Kart:
Niet začo. Neviem či ste si v rámci cvičení z analýzy (ak ste nejaké v dištančnej forme mali) túto formulku spomínali alebo nie, ale je veľmi užitočná, ako sám vidíš.
IMHO by našla uplatnenie aj v SŠ matematike, ale myslím že v rámci témy súčtových a rozdielových vzorcov goniometrických funkcií sa nespomína, a vlastne ani nikde inde.
Offline
#13 03. 04. 2021 10:56
Re: Integrovateľnosť f(x) na intervale
↑ Ferdish:
Bohužiaľ, nespomínali sme. Nerozumiem prečo, ak je to také užitočné
Offline
#14 09. 04. 2021 13:39
Re: Integrovateľnosť f(x) na intervale
↑ Kart:
pravdepodobne preto, ze za mojich cias sa to bezne ucilo na strednej skole a vysoke skoly asi pocitaju, ze to vsetci vedia
len by someste podotkol ze na zaklade ↑ laszky: sa to da vypocitat bez velkeho trapenia
ked dosadime  do
do  tak dostaneme
tak dostaneme  , teda zo spjitosti
, teda zo spjitosti  mame, ze existuje interval
mame, ze existuje interval  , na ktorom je
, na ktorom je  a teda funkcia
a teda funkcia  tam nie je definovana, takze nemoze byt integrovatelna na jeho nadintervale
tam nie je definovana, takze nemoze byt integrovatelna na jeho nadintervale ![kopírovat do textarea $[0,8]$](/mathtex/02/02733e8a7d327206c4232f97df879045.gif)
Offline
#16 09. 04. 2021 14:19 — Editoval Ferdish (09. 04. 2021 14:20)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Integrovateľnosť f(x) na intervale
↑ Brano:
Súhlasím, ale pre dnešného gymnazistu-maturanta resp. prváka na výške by však prípadná "obhajoba" toho, prečo ho zaujímajú hodnoty daného výrazu práve v týchto zvolených bodoch def. oboru resp. daného intervalu, trochu problematická. Koniec koncov ani ↑ laszky: to bližšie nešpecifikoval.
OK, pokiaľ sa jedná o v matematike viac než nadpriemerne zdatného študenta (na súčasné pomery), tak by sa v prípade bodu [mathjax]x=\frac{5\pi }{4}[/mathjax] dalo vychádzať z hodnoty globálneho minima funkcie [mathjax]f(x)=\sin x+\cos x=\sqrt{2}\sin (x+\frac{\pi }{4})[/mathjax] a od tejto myšlienky sa odvíjať, ale menej matematicky zdatného študenta to v ten okamih nenapadne, že...
Offline
#17 14. 04. 2021 17:12
Re: Integrovateľnosť f(x) na intervale
↑ Ferdish:
ja som spojil dve rozne veci dohromady a potom mi asi nebolo rozumiet :D
ta prva cast sa tykala toho vzorca; t.j. ze ako upravit  na
na  sa bezne ucilo na strednej skole; lebo nad tym sa ↑ Kart: pozastavoval, ze to nespominali a pritom to je uzitocne
sa bezne ucilo na strednej skole; lebo nad tym sa ↑ Kart: pozastavoval, ze to nespominali a pritom to je uzitocne
a potom ta druha cast prispevku sa tykala toho ineho pristupu, co mal laszky, ktory je mimo zaber strednej skoly, t.j. je ideovo pomerne narocny, ale technicky jednoduchsi na pouzitie v tomto konkretnom pripade. Preto si podla mna zasluzil dodatocny komentar.
Offline
#18 14. 04. 2021 17:43 — Editoval Ferdish (14. 04. 2021 17:44)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Integrovateľnosť f(x) na intervale
↑ Brano:
No ja si na ten vzorec (súčet a-násobku sínusu a b-násobku kosínusu) tiež nespomínam, a to som strednú končil roku 2008.
Čo sa dalo upraviť pomocou štandardných goniometrických súčtových a rozdielových vzorcov, sa upravilo.
Známe boli aj vzorce pre súčet a rozdiel funkcií s rôznymi argumentmi, jednoduchý zmiešaný súčet [mathjax]\sin x+\cos x[/mathjax] sme využili vo fyzike v kapitole o kmitoch a vlnách.
Na zmiešaný súčet funkcií s rôznymi argumentmi však nesedel ani jeden zo spomínaných vzorcov.
Na druhú stranu, nepamätám si či sme niekedy počítali nejakú úlohu, kde by to bol (vzhľadom na dostupnú "výzbroj") neriešiteľný problém.
Rozdiely v tom, čo sa v rámci matematiky preberalo na stredných školách a gymnáziách v SR a v ČR boli už vtedy.
Reforma školstva po mojich maturitách síce po... čo sa dalo, ale za tento konkrétny prípad nenesie vinu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrovateľnosť f(x) na intervale (TOTO TÉMA JE VYŘEŠENÉ)
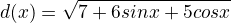 integrovateľná
integrovateľná 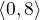 ? Svoje tvrdenie zdôvodnite.
? Svoje tvrdenie zdôvodnite.