Matematické Fórum

Flaky · 18. 05. 2021 11:27

Dobrý den,

chtěl bych se zeptat, jakým způsobem bych mohl ověřit absolutní konvergenci a stejnoměrnou konvergenci následující řady pro [mathjax]\xi \in (-R,R)[/mathjax] , kde [mathjax]R>0[/mathjax] je reálné číslo a funkce [mathjax]f: \mathbb{R} ->\mathbb{C}[/mathjax] je hladká a má kompaktní nosič.

Odkaz na zadání: https://pasteboard.co/K2rqxRD.png

Bati · 01. 06. 2021 11:41

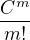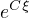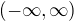Integral uvnitr muzes v absolutni hodnote odhadnout $\frac{C^m}{m!}$ , a tudiz cely soucet je v abs. hodnote mensi nez $e^{C\xi}$ , kde $C$ je nejaka konstanta zavisejici na $f$ . Z toho je patrne, ze rada je stejnomerne konvergentni pouze lokalne v $(-\infty,\infty)$ , podobne jako Taylorova rada funkce $e^x$ .

Matematické Fórum

#1 18. 05. 2021 11:27

Konvergence řady

#2 01. 06. 2021 11:41

Re: Konvergence řady

Zápatí