Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 06. 2021 13:42
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1150
- Reputace: 19
- Web
mocniny v komplexním oboru
V reálném oboru je např. x^(1/2)=x^(2/4)
V komplexním oboru to není tak úplně pravda, tam je n-tá odmocnina n- značná.
Víceznačná funkce x^(1/2) má užší sortiment než funkce x^(2/4).
Např. (-1)^(1/2) = i, - i,
Např. (-1)^(2/4)=1^(1/4) = 1; -1; i; -i;
Tedy x^(1/2) není v komplexním oboru úplně totéž, co x^(2/4).
Offline
#4 15. 06. 2021 22:18
Re: mocniny v komplexním oboru
↑ Richard Tuček: , ale
, ale  . Delas stejnou chybu jako ve znamem "dukazu", ze -1=1.
. Delas stejnou chybu jako ve znamem "dukazu", ze -1=1.
Offline
#5 16. 06. 2021 12:00
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1150
- Reputace: 19
- Web
Re: mocniny v komplexním oboru
↑ Bati:
Ten "důkaz" samozřejmě znám.
1=odm(1)=odm((-1)*(-1))=i*i=-1
První rovnost je v reálném oboru správná, ale v komplexním je pofiderní (tam je druhá odmocnina dvojznačná).
Mezi zlomky platí rovnost (1/2)=(2/4), ale v komplexním oboru x^(1/2) není úplně přesně totéž, co x^(2/4).
V reálném oboru je sudá odmocnina jednoznačná, pokud přijmeme konvenci, že za sudou odmocninu z kladného čísla se bere kladné číslo.
Proto také v reálném oboru platí: odm(x^2)=abs(x) (také jsem si to kdysi neuvědomil).
Offline
#6 16. 06. 2021 15:10
Re: mocniny v komplexním oboru
Poznamka.
Toto sa oplati kuknut: https://en.wikipedia.org/wiki/Mathematical_fallacy .
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 16. 06. 2021 23:42
Re: mocniny v komplexním oboru
↑ Richard Tuček:
Nemas pravdu, resp. vidis problemy tam, kde nejsou. Protoze 1/2=2/4, tak plati  pro libovolnou funkci
pro libovolnou funkci  , klidne i mnohoznacnou, to je irrelevantni. Z definice racionalnich cisel jsou 1/2 a 2/4 ty same objekty. Tolik k
, klidne i mnohoznacnou, to je irrelevantni. Z definice racionalnich cisel jsou 1/2 a 2/4 ty same objekty. Tolik k  .
.
Co se tyce  , nebo ekvivalentne
, nebo ekvivalentne  , nejprve je jasne, ze na leve strane je nutne pouzit obecnejsi definici mocniny:
, nejprve je jasne, ze na leve strane je nutne pouzit obecnejsi definici mocniny: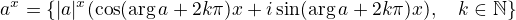 , kde
, kde 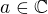 ,
, 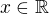 a
a 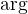 vraci argument komplexniho cisla lezici v
vraci argument komplexniho cisla lezici v 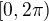 . Tudiz
. Tudiz 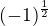 je dvouprvkova mnozina. Ale na prave strane
je dvouprvkova mnozina. Ale na prave strane 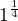 je bud
je bud  (pokud pouzijeme realnou odmocninu), anebo ctyrprkova mnozina, pouzijeme-li definici komplexni. Takze
(pokud pouzijeme realnou odmocninu), anebo ctyrprkova mnozina, pouzijeme-li definici komplexni. Takze 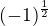 se nemuze rovnat
se nemuze rovnat 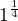 uz jen proto, ze to jsou neporovnatelne objekty. V reci programovani to odpovida tomu, ze nesedi typy (a neexistuje zadne rozumne implicitni pretypovani).
uz jen proto, ze to jsou neporovnatelne objekty. V reci programovani to odpovida tomu, ze nesedi typy (a neexistuje zadne rozumne implicitni pretypovani).
Jinak debaty tohoto typu podle me nejsou moc uzitecne, protoze v kazdem serioznim textu by melo byt dopredu deklarovano (anebo to musi byt jasne z kontextu), co se mysli zapisem 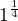 apod.
apod.
Ahoj ↑ vanok:, na te wiki v te casti "Square roots of negative numbers" to maji taky spatne (uz jen 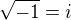 ), takze to necist.
), takze to necist.
Offline
#8 17. 06. 2021 06:04
Re: mocniny v komplexním oboru
Ahoj ↑ Bati:
Len mala poznamka..
Uz len titul toho odkazu znamena, ze ide « pseudo » dokazy a iste autory chceli tam dat ilustraciu spatnych dokaov.
Mozno mohli na to viac prizvukovat…
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 17. 06. 2021 15:40
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1150
- Reputace: 19
- Web
Re: mocniny v komplexním oboru
Pozor:
Také rovnosti: i^2=-1; i=odm(-1); nejsou úplně ekvivalentní, neboť druhá odmocnina je dvojznačná.
Jistý docent (machr v analýze v komplexním oboru) napsal knihu Analýza v komplexním oboru, je to tlustá kniha (autor I. Černý)
Pravil: "nesmíme mísit metody reálné a komplexní analýzy"
Offline