Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 07. 2021 20:30
Tretia mocnina
Pozdravujem,
Dokazte, ze kazde cele cislo formy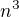 
je rozdiel dvoch celych cisiel formy 
. ( 
je cele cislo).
Priklad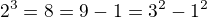 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 08. 07. 2021 15:20 — Editoval Honzc (08. 07. 2021 18:04)
Re: Tretia mocnina
Offline
#3 08. 07. 2021 20:47
Re: Tretia mocnina
Ahoj ↑ Honzc:,
Pekne stredoskolske riesenie 👍.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 09. 07. 2021 10:28 — Editoval vanok (09. 07. 2021 10:29)
Re: Tretia mocnina
Poznamka:
Ine riesenie.
Moze sa vyuzit znamy (?) vzorec [mathjax]1^3+…+n^3=…[/mathjax]
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 09. 07. 2021 12:20
Re: Tretia mocnina
Ahoj ↑ Honzc:,
Pochopitelne ( a niekomu sa to moze zdat velmi prirodzene!).
A este, amatery matematickej indukcie mozu ju tiez pouzit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 09. 07. 2021 19:03 — Editoval check_drummer (09. 07. 2021 19:04)
- check_drummer
- Příspěvky: 4781
- Reputace: 105
Re: Tretia mocnina
↑ Honzc:
Ahoj. To nejzajímavější, tj. jak jsme dospěli k tomu vyjádření x a y, bohužel chybí. Ale tento jev se často v učebnicích vyskytuje, kde zvolíme nějaký tvar výrazu, který jakoby spadl z nebe, a pro něja pak řešení jakoby zázrakem získáme.
v totmo případě lze ale volbu x,y snadno zdůvodnit:
"Máte úhel beta." "No to nemám."
Offline
#8 09. 07. 2021 19:05
- check_drummer
- Příspěvky: 4781
- Reputace: 105
Re: Tretia mocnina
↑ vanok:
Ahoj. Že by bylo možné ten vzorec nějak využít mě napadlo hned, ale až teď to použití vidím. :-) Je to snadné.
"Máte úhel beta." "No to nemám."
Offline
#9 09. 07. 2021 20:08
- check_drummer
- Příspěvky: 4781
- Reputace: 105
Re: Tretia mocnina
Vlastně by se tak dal i ten součtový vzorec tímto postupem dokázat.
"Máte úhel beta." "No to nemám."
Offline