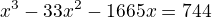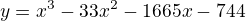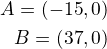#1 17. 07. 2021 08:03
Pomoc s vypoctom
Mohli by ste mi prosim pomoct s vypoctom
1) Upraviť kubickú rovnicu do základného tvaru:
2x^3 + 4x^2 - 226 - 521x -14x + 15x^2 = 22 + 4x + 21x^2 + (5x^3)/3 + 9x^2 + 16x
2) Rovnicu zapíšte ako funkciu a následne derivujte
3) Určte priesečníky zderivovanej funkcie s osou x
4) Priesečníky označíte ako A , B , kde A má súradnice [a,0] a B [b,0] a zároveň platí nerovnosť a<b
Dostal som sa zatial k tomuto. Aj to neviem ci spravne.
2x^3+19x^2−535x−226=0
x1 = 12.543670162534
x2 = -21.627131912008
x3 = -0.41653825052609
Dakujem
Offline
