Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Indefinite integration with natural logarithms
#4 16. 08. 2021 17:36
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Indefinite integration with natural logarithms
↑ Bati:
Ahoj. Zajímavé je, že funkce i její primitivní funkce mají hodně podobný tvar.
"Máte úhel beta." "No to nemám."
Offline
#5 16. 08. 2021 20:54
Re: Indefinite integration with natural logarithms
↑ check_drummer:
Ahoj, je to tak, konkretne funkce
resi ODR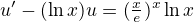 ,
,  .
.
I takto se ten integral da "pocitat".
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Indefinite integration with natural logarithms

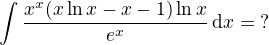
![kopírovat do textarea $ \ \int\frac{x^x(x\ln x-x-1)\ln x}{e^x}\,\mathrm{d}x=\int e^{x(\ln x-1)}(x(\ln x-1) -1) \ln x dx =\\
\ =[t=x(\ln x-1)]=\int e^t(t-1)dt=...$](/mathtex/cb/cbfc31105d2bdc9786f9d222af465653.gif)