Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Regularita slabeho riesenia parcialnej rovnice
#1 13. 08. 2021 22:26
Regularita slabeho riesenia parcialnej rovnice
Zdravim,
chcel by som sa len spytat, preco sa vlastne v teorii parcialnych diferencialnych rovnic zaobera regularitou slabych rieseni. Ma to nejake vyuzitie niekde? (vo fyzike, alebo tak...)
Popripade ak by mi niekto vedel odporucit nejaku literaturu, kde to je popisane, tak by som bol vdacny.
Offline
#2 16. 08. 2021 23:34
Re: Regularita slabeho riesenia parcialnej rovnice
Ahoj,
to je dobra otazka. Jestli ma regularita vyuziti ve fyzice zavisi na tom, jak dobre PDR popisuje zkoumany fyzikalni system a taky jak presne umime experimentalne merit. Je potreba mit na pameti, ze PDR se musi odvodit z nejakych predpokladu a to vzdycky bude zahrnovat nejakou aproximaci. Uz jenom proto, ze PDR se tykaji kontinua, kdezto (detailni) fyzika zahrnuje malinkate castice. V idealnim pripade, pokud vime, ze mame relativne presna data, presny model a konstanty v odhadech regularity jsou mnohem mensi nez pocet atomu ve vesmiru, tak se da regularita vztahnout na realitu. To znamena, ze napr. ze spojitosti reseni cteme, ze nevznikaji razove vlny apod. Je tu ale hacek: Clovek muze vzit nejakou osklivou PDR, ktera sice ma reseni v nejakem smyslu, ale pro kterou zadna regularita dokazat nejde. A ted si na levou stranu pridam treba 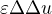 . To mi nejspis dost pomuze s regularitou a navic muzu doufat, ze kdyz
. To mi nejspis dost pomuze s regularitou a navic muzu doufat, ze kdyz  zvolim hodne maly, dostane se chyba modelu pod rozlisovaci schopnosti fyzikalniho mereni. To naznacuje, ze spis nez zkoumat regularitu nahodnych PDR je zajimavejsi studovat regularitu tech PDR, ktere maji jasne fyzikalni opodstatneni (v podstate Occamova britva) a vysledky pak porovnat s experimentalnim pozorovanim. Takze v podstate smyslem je overit, jestli dana PDR (model) skutecne vykazuje vlastnosti konzistentni s pozorovanim ve skutecnosti. Pokud ano, zvysuje to verohodnost naseho modelu.
zvolim hodne maly, dostane se chyba modelu pod rozlisovaci schopnosti fyzikalniho mereni. To naznacuje, ze spis nez zkoumat regularitu nahodnych PDR je zajimavejsi studovat regularitu tech PDR, ktere maji jasne fyzikalni opodstatneni (v podstate Occamova britva) a vysledky pak porovnat s experimentalnim pozorovanim. Takze v podstate smyslem je overit, jestli dana PDR (model) skutecne vykazuje vlastnosti konzistentni s pozorovanim ve skutecnosti. Pokud ano, zvysuje to verohodnost naseho modelu.
Pokud mas na mysli literaturu tykajici se presne teto otazky (k cemu to je), tak nevim. Jinak ohledne regularity samotne se muzeme bavit dal, ale to jsi asi nechtel...
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Regularita slabeho riesenia parcialnej rovnice
