Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 05. 2017 16:17
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Dokazatelnost podivné (ne)rovnosti
Ahoj,
inspirován jiným vléknem zde, zadávám tento dotaz. Tvrzení, která budeme zkoumat, jsou myšlena čistě formálně - tj. jako syntaktické výroky. Uvažujme, že se pohybujeme v nějakém obecném tělese T (tj. t je dáno jako nějaká běžná množina axiomů popisujících těleso).
1) Je (v T) dokazatelé 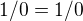 ?
?
20 Je (v T) dokazatelné  (tj. negace předchozího výroku)?
(tj. negace předchozího výroku)?
Upozorňuji, že mi jde o syntaktickou dokazatelnost (ve smyslu "odovozování řetězců z jiných řetězců" - kde tyto řetězce pokládáme za dokazatelné výroky), tj. tvrzení, že "nulou dělit nelze" samo o sobě nelze považovat za "důkaz".
Nabízím řešení k diskusi:
"Máte úhel beta." "No to nemám."
Offline
#2 27. 05. 2017 16:00 — Editoval check_drummer (27. 05. 2017 16:04)
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Dokazatelnost podivné (ne)rovnosti
Ahoj,
jeví se mi to tak, že platí jedno z následujících:
1) Znak pro dělení není součástí jazyka okruhu a tedy výraz 1/0 nemá smysl a tudíž ani uvedené výroky smysl nemají a tedy nemá smysl se bavit o jejich dokazatelnosti.
2) Znak pro dělení je sice součástí jazyka okruhů, ale některé výrazy nejsou povoleny, např. výrazy a/0, případně obecně výrazy a/b, kde je dokazatelné, že b=0.
Ponámka: Kdyby platil bod 1, pak bychom spoustu pěkných tvrzení nemohli formulovat, resp. museli bychom je složitě opisovat pomocí znaku násobení. Ale pro naše účely bych si v tom případě vybral nějakou jinou strukturu, např. s funkcí log a zkoumal bych třeba ("nedefinovaný") výraz log(0) - čímž bych bod 1 převedl na bod 2 (případně na bod 3).
3) Jsou povoleny i výrazy 1/0 (v syntaktickém smyslu, tj. jako "řetězce") a výroky, ve kterých se tyto výrazy vyskytují, lze zkoumat standardními postupy týkajícími se "dokazatelností". Tady se ale obávám, že by bylo možné dokázat nejen, že 1/0=1/0, ale např. i substitucí 1/0 do nějaké platné identity, např. že 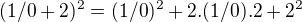 . No ale proč ne? :-)
. No ale proč ne? :-)
Ale v tomto případě tedy z vlastností predikátu rovnosti nebude dokazatelné  .
.
A jak to bude v bodě 3 s modelem (ve kterém by platilo 1/0=1/0)? O tom jsem nepřemýšlel, tak v krátkosti: Možná by ten model mohl mít samostatné individuum pro výraz 1/0. Případně žádný takový model uvedené struktury neexistuje - což by pak ale asi znamenalo, že je v té struktuře dokazatelné každé tvrzení, protože je platné ve všech modelech. :-) Takže struktura bez modelu je nezajímavá (sporná).
Tak asi tak, stále se nebráním diskusi. :-)
"Máte úhel beta." "No to nemám."
Offline
#3 01. 09. 2021 18:08 — Editoval Wotton (01. 09. 2021 18:29)
Re: Dokazatelnost podivné (ne)rovnosti
Krásné, trochu mě to potrápilo, ale nakonec mám zdá se odpověď:
Beru to z pohledu logiky (v tělesech jsem jaště slabší).
Je třeba se zamyslet nad tím, co znamená výraz [mathjax]a/b[/mathjax]. Tento výraz je vlastně zkratka za takový prvek univerza [mathjax]z[/mathjax] pro který platí: [mathjax]z=a/b \wedge\forall x (x=a/b \Rightarrow x=z)[/mathjax], pokud takový prvek existuje.
Zcela syntakticky správně by pak rovnice [mathjax]a/b = c/d[/mathjax] měla vypadat[mathjax2]
\exists x\exists y((x=a/b\wedge \forall u(u=a/b\Rightarrow x=u))\wedge(y=c/d\wedge \forall v(v=c/d\Rightarrow y=v))\wedge x=y)
[/mathjax2]
po dosazení za [mathjax]a[/mathjax] [mathjax]b[/mathjax] [mathjax]c[/mathjax] [mathjax]d[/mathjax] pak (při nějaké standardní axiomatizaci fonktoru [mathjax]/[/mathjax]) je pak zjevně dokazatelná negace.
pokud bys ale nechtěl přistoupit na až tak hluboký stupeň formalizace, tak ti nezbyde než konstatovat, že výraz [mathjax]1/0[/mathjax] (z důvodu uvedeným výše) nedává smysl, tudíž nelze o rovnosti [mathjax]1/0 = 1/0[/mathjax] vůbec uvažovat.
Dva jsou tisíckrát jeden.
Offline
#4 01. 09. 2021 18:16
Re: Dokazatelnost podivné (ne)rovnosti
↑ Wotton:
a teď mi k tomu došlo, že to je krásná ukázka toho, že neplatí ekvivalence výroků [mathjax2]1/0 \not = 1/0[/mathjax2] a [mathjax2]\neg(1/0 = 1/0)[/mathjax2]. (první je vyvratitelný a druhý dokazatelný - při standardní axiomatizaci dělení)
Dva jsou tisíckrát jeden.
Offline
#5 01. 09. 2021 23:22
Re: Dokazatelnost podivné (ne)rovnosti
Já na takové složitosti nejsem, ale z mého pohledu je ten operátor / prostě zobrazení definované podle
c=a/b => a = b*c
a pokud taková čísla nelze najít, tak prostě není definován.
No a když bychom chtěli množinu těch čísel rozšířit, podobně, jako jsme vymysleli imaginární čísla, že by se řeklo, že třeba
[mathjax]x = 1/0[/mathjax]
tak se hned dostaneme ke sporům, protože pak by muselo platit, že
x = 1/0
5x = 5/0
takže
x * 0 = 1
5 * x * 0 = 5
Jenže my potřebujeme aby bylo násobení komutativní a asociativní, takže pravé strany se musí rovnat,
x * 0 = 1
x * (0 * 5) = 5
A máme tu ten spor. Takže takový symbol nemůžeme jednoduše zavést, narozdíl od té odmocniny z -1, pro kterou všechno krásně funguje.
Takže jestli tomu rozumím správně, tak předpokladem, že výraz 1/0 můžeme vytvořit si zavedeme do systému spor, a pak už v něm lze obecně dokázat i vyvrátit kde co...
Takže podle mě je jediný správný únik ten, že to prostě nesmíme udělat.
Offline
#6 02. 09. 2021 14:33
Re: Dokazatelnost podivné (ne)rovnosti
↑ MichalAld:
to ale nelze tak jednoduše udělat, dokud se bavíme jen o syntax jak chtěl na začátek kolega.
Dva jsou tisíckrát jeden.
Offline
