Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Analytická geometrie - výpočet úhlu mezi dvěma přímkami (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 09. 2017 18:30
Analytická geometrie - výpočet úhlu mezi dvěma přímkami
Zdravím,
jak byste vyřešili následující úlohu? (povolena je pouze tužka a papír):
Jaký úhel svírá přímka procházející body [1,1] a [−3,−3] s vektorem (−3, √3)?
Odpověď je: 
Jak jsem postupoval:
Úhel jsem počítal přes skalární součin, ale jelikož není povolena kalkulačka, abych použil inverzní funkci cosinus, použil jsem vzorec pro poloviční úhel.
1. Nejprve jsem si zjistil směrový vektor dané přímky, což je (1, 1)
2. Poté jsem použil skalární součin:

3. Poté jsem tento výraz upravil tak, aby odpovídal vzorci pro poloviční úhel
Vzorec:

Úprava:

A tedy:

4. Podle vzorce pro poloviční úhel je alpha/2 = pi/12:


5. Když se vrátíme na začátek výpočtu, tak si všimneme, že sinus tohoto úhlu je roven cos(x):

6. Podle vzorce sin(a) = cos(a - pi/2) převedeme náš sinus na cosinus:

7. Úhel, který svírají dané přímky, je tedy 5pi/12:


Offline
- (téma jako vyřešené označil(a) lddangsta)
#2 18. 09. 2017 20:27
Re: Analytická geometrie - výpočet úhlu mezi dvěma přímkami
↑ lddangsta:
Proti gustu ...
já bych pokračoval

Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 18. 09. 2017 20:34
Re: Analytická geometrie - výpočet úhlu mezi dvěma přímkami
↑ lddangsta:
A já bych si to namaloval, všiml si, že přímka svírá s osou x úhel 45 stupňů, a protože vím, že  , je to už jen o sečtení těch dvou čísel. On je celý postup totiž dost závislý na tom, jaké hodnoty goniometrických funkcí znám nebo neznám.
, je to už jen o sečtení těch dvou čísel. On je celý postup totiž dost závislý na tom, jaké hodnoty goniometrických funkcí znám nebo neznám.
Offline
#4 19. 09. 2017 07:29 — Editoval Cheop (19. 09. 2017 07:36)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Analytická geometrie - výpočet úhlu mezi dvěma přímkami
↑ lddangsta:
No nevím, ale vychází  protože:
protože: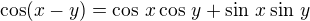
Nikdo není dokonalý
Offline
#6 19. 09. 2017 13:04
Re: Analytická geometrie - výpočet úhlu mezi dvěma přímkami
↑ zdenek1:To je hodně zajímavej postup, to by mě nikdy nenapadlo, děkuji.
Offline
#8 24. 09. 2021 00:33 — Editoval Mathstudent (24. 09. 2021 00:34)
- Mathstudent

- Zelenáč
- Příspěvky: 12
- Pozice: student
- Reputace: 0
Re: Analytická geometrie - výpočet úhlu mezi dvěma přímkami
↑ zdenek1:
Mohl by mi prosim nekdo vysvetlit tuto upravu, kterou jste provedl ve druhem kroku do souctoveho vzorce?
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Analytická geometrie - výpočet úhlu mezi dvěma přímkami (TOTO TÉMA JE VYŘEŠENÉ)
 .
. ? Jinak asi nejrychlejší způsob, díky.
? Jinak asi nejrychlejší způsob, díky.