Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Laplaceova rovnice, okrajové podmínky
#1 16. 09. 2019 15:05
Laplaceova rovnice, okrajové podmínky
Dobrý den, chtěl bych se zeptat zda-li je analyticky možné řešit následující úlohu PDR: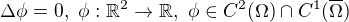 , se smíšenými okrajovými podmínkami (dvě Dirichletovy a dvě Neumannovy), kde oblast je ohraničena čtyřmi křivkami, které jsou v bodech průniku ortogonální. Hranice je tedy například obdélník nebo část mezikruží. Napadlo mě využít metodu potenciálů, ale ta zřejmě vyžaduje hladkou hranici, což v tomhle případě neplatí, nebo Fourierovu metodu řad, ale ta se obvykle používá v polárních souřadnicích. Za jakoukoliv pomoc budu vděčný.
, se smíšenými okrajovými podmínkami (dvě Dirichletovy a dvě Neumannovy), kde oblast je ohraničena čtyřmi křivkami, které jsou v bodech průniku ortogonální. Hranice je tedy například obdélník nebo část mezikruží. Napadlo mě využít metodu potenciálů, ale ta zřejmě vyžaduje hladkou hranici, což v tomhle případě neplatí, nebo Fourierovu metodu řad, ale ta se obvykle používá v polárních souřadnicích. Za jakoukoliv pomoc budu vděčný.
Offline
#2 16. 09. 2019 19:18
Re: Laplaceova rovnice, okrajové podmínky
ahoj ↑ duskin:
toto je uz pre mna velmi davno, ale ak si dobre spominam
tak kazda jednoducho suvisla podmnozina v 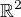 s aspon po castiach hladkou hranicou
s aspon po castiach hladkou hranicou
sa da transformovat na jednotkovy kruh zobrazenim ktore v istom zmysle "zachova strukturu domeny"
v zavislosti od toho ako realne vyzera tvoja oblast moze a nemusi byt lahke najst
taku transformaciu suradnic
tak na uvod by som mozno pozrel nieco o konformnych zobrazeniach
alebo metode konformnych zobrazeni pre Laplaceov okrajovy problem,
mohlo by ta to posunut dalej, ziadny material ma z hlavy nenapada
pripadne ma hadam doplni nejaky kolega
Offline
#4 12. 12. 2022 20:53
Re: Laplaceova rovnice, okrajové podmínky
Založ si nové vlákno a napiš, co tě trápí... zadání typu "řešte diferenciální rovnice" je podle mě tak trochu neřešitelné...
Ještě bych podotkl, že Laplaceova transformace a Laplaceova rovnice je každé něco úplně jiného.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Laplaceova rovnice, okrajové podmínky
