Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Analytická geometrie - Trojuhelník (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 06. 2009 19:37 — Editoval Zbyšek (30. 06. 2009 20:02)
Analytická geometrie - Trojuhelník
Je dán trojuhelník se souřadnicemi: A=[3;-5], B=[1;4], C=[-6,2]
Vypočtěte:
a) velikost strany b
b) rovnici strany b
c) velikost výšky vb
d) úhel beta
e) rovnoběžku se stranou c procházející počátkem O
f) rovnoběžku s osou x procházející bodem B
g) těžiště T
Postupně sem dodám výpočet pro kontrolu, ale nevím jak postupovat u výpočtu těžiště.
Díky za rady :]
Edit: Teď mě napadlo že by možná to těžiště šlo vypočítat pomocí rovnic středů stran. Vypočítat tři rovnice a pak je pomocí sčítací nebo dosazovací metody vypočíst.
Offline
#4 01. 07. 2009 10:38 — Editoval Cheop (02. 07. 2009 14:32)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Analytická geometrie - Trojuhelník
↑ Zbyšek:
Pokud jsem dobře počítal: (pro kontrolu)
a) b = sqrt(130) = 11,4 (cca)
b) 7x + 9y + 24 = 0
c) v_b = 5,88(cca)
d) beta = 86 stupňů 35 minut
e) 9x + 2y = 0
f) y - 4 = 0
g) T(-2/3; 1/3)
Obrázek:
Nikdo není dokonalý
Offline
#6 01. 07. 2009 18:40 — Editoval Chrpa (01. 07. 2009 18:57)
Re: Analytická geometrie - Trojuhelník
↑ Zbyšek:
No já to počítal takto:
Výška je kolmá ke straně b (prochází bodem B)
Určil jsem tedy rovnici v_b
a průsečík se stranou b
Délka je potom vzdálenost průsečíku výšky se stranou a bodem B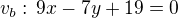
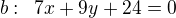
Řešíš tyto 2 rovnice a zjistíš průsečík. P
A pak určíš vzdálenost BP což je délka výšky.
PS: Možná to jde i jinak.
Mě však nic jiného nenapadlo.
Offline
#7 01. 07. 2009 19:15 — Editoval Zbyšek (01. 07. 2009 19:24)
Re: Analytická geometrie - Trojuhelník
Nalezl jsem způsob jak to vypočíst možná i jednodušeji, jedná se o to, že se vypočte rovnice strany b do té se za xy dosadí hodnoty bodu B a vydělí se 17 pod odmocninou.
např:
x+4y+11=0 (rovnice strany b)
B=[1,5]
Vb =1+20+11/odmocnina z 17
Ted jen nevím jak získat tu hodnutu "17" jestli je pro všechny trojuhelníky stejná, nebo jestli se vypočítává podle nějakého vzorečku.
VYŘEŠENO:
Tak to mám :]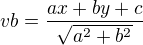
Offline
#8 01. 07. 2009 19:23
- marnes

- Příspěvky: 11227
Re: Analytická geometrie - Trojuhelník
↑ Zbyšek:To jsi dosazoval do vzorce pro vzdálenost bodu od přímky. Ta odmocnina je velikost normálového vektoru, v tomto případě (1;4) (1^2+4^2=17 a z toho odmocnina), takže pro každou obecnou rovnici přímky je to ve jmenovateli jiné!!!
Jo. A na začátku vás zdravím.
Offline
#10 03. 07. 2009 10:40 — Editoval Cheop (03. 07. 2009 11:44)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Analytická geometrie - Trojuhelník
Jen tak pro zajímavost jak složitě jde počítat případ c) z tohoto dotazu:
Zadáno:- trojúhelník zadán body:
A=[3;-5], B=[1;4], C=[-6,2] máme určit velikost v_b
Můj výpočet:
1) určím rovnici strany b
2) určím rovnici v_b
3) určím průsečík obou přímek P
4) určím vzdálenost BP
1) prochází body A, C tedy:
prochází body A, C tedy: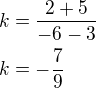 dopočítám q
dopočítám q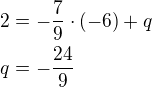
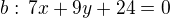 rovnice strany b
rovnice strany b
2)
v_b je kolmá na stranu b rovnice tedy bude: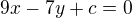 dosazením bodu B dopočítám c
dosazením bodu B dopočítám c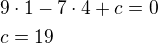
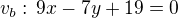 rovnice v_b
rovnice v_b
3)
Řeším rovnice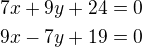 řešením je P:
řešením je P:![kopírovat do textarea $P\left[-\frac{339}{130}\,;\,-\frac{83}{130}\right]$](/mathtex/25/25056441f9709f360c96c69f55a2ef05.gif)
4)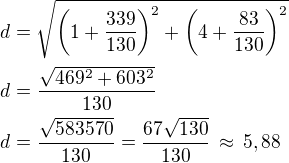
Jednodušší způsob výpočtu:
1) určení rovnice strany b
2) určení výšky v_b (jako vzdálenost bodu B od strany b)
1) stejný postup jako v prvním případě. tedy: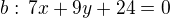
2)
v_b prochází bodem B takže souřadnice bodu dosadím do: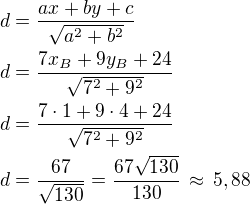
Výsledek je jak vidno stejný.
Nikdo není dokonalý
Offline
#13 03. 08. 2009 09:38 — Editoval Cheop (03. 08. 2009 10:21)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Analytická geometrie - Trojuhelník
↑ Zbyšek:
h1) prochází body A, C tedy:
prochází body A, C tedy: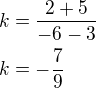 dopočítám q
dopočítám q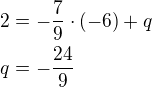
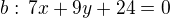 rovnice strany b
rovnice strany b
h2)
v_b je kolmá na stranu b rovnice tedy bude: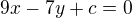 dosazením bodu B dopočítám c
dosazením bodu B dopočítám c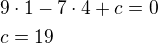
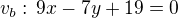 rovnice v_b
rovnice v_b
g)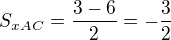
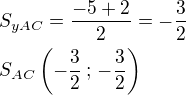
Vzdálenost S_AC od B = délka těžnice t_b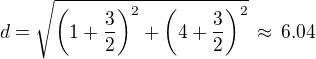
Nikdo není dokonalý
Offline
#14 03. 08. 2009 09:51
Re: Analytická geometrie - Trojuhelník
Offline
#17 13. 08. 2009 19:42
Re: Analytická geometrie - Trojuhelník
Určete délku těžnice na stranu BC v trojúhelníku ABC, je-li dáno :
A = [7;-5], B = [15;-4], C = [13;-8]
je to jedna casti pocitani prikladu z vektoru vypocital jsem vse jen teznici ne nevim jak nani nebo jsem ji pocital spatne"! muze te mi pomoct?
kdyby fyzika a matika zila tak uz jsem asi v base za vrazdu"!
Offline
#18 13. 08. 2009 19:47
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Analytická geometrie - Trojuhelník
↑ Julo88:Ta těžnice spojuje bod A se středem S strany BC. Jaké souřadnice má S? Jak pomocí souřadnic A a S určíme délku |AS| dané těžnice?
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#20 13. 08. 2009 20:22
Re: Analytická geometrie - Trojuhelník
Určete souřadnice vrcholů L a M a délku těžnice na stranu LM v trojúhelníku KLM, který je shodný s trojúhelníkem ABC ≈ KLM, je-li dáno :
A = [-3;2], B = [5;3], C = [3;-1] a K = [7;-5]. { [15;-4]; [13;-8]; }
to je ten cely priklad
kdyby fyzika a matika zila tak uz jsem asi v base za vrazdu"!
Offline
#21 13. 08. 2009 21:21
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Analytická geometrie - Trojuhelník
↑ Julo88:Teď nevím, jestli jsme se pochopili. Za S jsem položil (B+C)/2, délka těžnice |SA| se spočítá tak, že nejprve určíš vektor S-A a následně spočítáš jeho velikost (dle Pythagorovy věty).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#22 13. 08. 2009 21:25
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Analytická geometrie - Trojuhelník
↑ Julo88:Co má znamenat to { [15;-4]; [13;-8]; }? a ABC ≈ KLM značí shodnost? Takže o KLM víme, jak má být velký, víme, kde má vrchol K, ale nevíme, jak má být natočen? Jinak délka těžnice na LM v KLM je stejná jako délka těžnice na BC v ABC.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Analytická geometrie - Trojuhelník (TOTO TÉMA JE VYŘEŠENÉ)
 procházející bodem B.
procházející bodem B.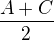
![kopírovat do textarea $T\left[\frac{a_1+b_1+c_1 }{3};\frac{a_2 +b_2 +c_2 }{3};\frac{a_3 +b_3 +c_3 }{3}\right]$](/mathtex/60/607754fecd57ba02039e53da81053f76.gif)
![kopírovat do textarea $T\left[\frac{a_1+b_1+c_1 }{3};\frac{a_2 +b_2 +c_2 }{3}\right]$](/mathtex/0c/0cf5d8539ea947abc6a0baca1b05ff6d.gif)