Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Metoda nejmenších čtverců (TOTO TÉMA JE VYŘEŠENÉ)
#5 23. 06. 2009 16:09 — Editoval lukaszh (23. 06. 2009 16:15)
Re: Metoda nejmenších čtverců
Ginco napsal(a):
↑ kotry:
tak to je polynomkde a2 a1 a0 jsou konstanty
Tak toto je kvadratická rovnica. My nehľadáme korene polynómu, ale polynóm samotný. Polynóm druhého stupňa je
↑ kotry:
Známa je hlavne regresná priamka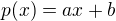
pričom koeficienty a,b som rozpisoval tu http://forum.matweb.cz/viewtopic.php?id=7730 Podobný postup skús aplikovať nie na polynóm prvého stupňa (priamku) ale na parabolu.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#6 23. 06. 2009 16:21
#8 23. 06. 2009 20:45
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Metoda nejmenších čtverců
ano
Offline
#9 01. 07. 2009 13:02
Re: Metoda nejmenších čtverců
našel by se PLS někdo kdo by spočítal tento příklad a dal sem postup ??
Metodou nejmenších čtverců určete funkci f(x), která nejlépe aproximuje naměřené hodnoty
zkoušel jsem to podle těch vzorečků, ale nevychází to.
tady jsem našel že to jde počítat i pomocí matice ale nepřišel jsem na to jak
http://cs.wikipedia.org/wiki/Metoda_nej … Dch_rovnic
http://cmp.felk.cvut.cz/cmp/courses/rec … node2.html
(výsledek f(x) = x^2 + 2x + 3 )
Offline
#10 01. 07. 2009 17:52
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Metoda nejmenších čtverců
↑ kotry:
Zdravím,
mám za to, že "dlužím" za zaslání sbírky zadání k elektrotechnice (děkuji :-), je to tak?
Tak jsem pomocí EXCEL a WIMS dala dohromady (moc se omlouvám za úpravu, ale pochybuji, že se mi bude chtit tvorit neco lepsího - pouze, pokud to je velmi nesrozumitelné):
http://forum.matweb.cz/upload/1246463083-kotry.JPG
dosazeno do 3 vzorců, co uvádiš o příspěvek výš:
6*a+3*b+19*c=-31
3*a+19*b+27*c=2
19*a+27*b+115*c=-118
je potřeba řešit soustavu rovnic - pomocí wimsje výsledek:
http://wims.unice.fr/wims/wims.cgi?sess … amp;parms=
{ a = -3, b = 2, c = -1 }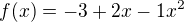
Podle zadani dat v tabulce parabola ma byt otocena vetve dolu / proto si myslim, ze vysledek, ktery uvadis, neni v poradku.
Stačí takto, případně se ptej. OK?
Offline
#11 01. 07. 2009 19:05 — Editoval kotry (01. 07. 2009 19:09)
Re: Metoda nejmenších čtverců
ohledně té paroboly nevím, právě že už takhle to vyšlo i spolužákovi. Ale je možné že výsledek je špatně-když už to vyšlo dvakrát
díky!
ještě když by to byl polynom 1. stupně, jaká by tam byla rovnice(vzorec) ?
jelena napsal(a):
↑ kotry:
... sbírky zadání k elektrotechnice (děkuji :-), je to tak?
Není za co ;-)
Offline
#12 01. 07. 2009 19:32 — Editoval jelena (01. 07. 2009 19:36)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Metoda nejmenších čtverců
↑ kotry:
Shoda se spolužákem je opravdu silný argument, ale ohledně té paraboly má být jasno již ze SŠ :-)
Parabola, která je uvedena ve výsledku (výsledek f(x) = x^2 + 2x + 3 ), má před kvadratickým členem kladné číslo (1), vetvě paraboly nahoru - otcovský web o tom podrobně pojednává.
Data, která jsou uvedena v tabulce v zadání, stačí naznačit na graf a je zřejmé, že se to podobá parabole se záporným číslem před kvadratickým členem. Stejně tak, pokud se nakreslí výsledná funkce, kterou jsme aproximovali.
Ostatně, je vhodné buď pouhým pohledem na tabulku nebo grafickým náznakem bodů zhodnotit, čim se dá nejlépe aproximovat. V tomto případě polynom 2. stupně je dobrá volba.
Pokud se má aproximovat lineárně, tak se dostaneme na zápis funkce: 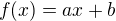
Vzorce pro nalezení koeficientů a, b jsou v soustavě, kterou máme k řešení - kopírováno odsud:
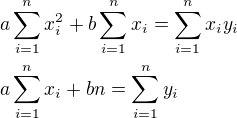
Je jasne, kterých sloupců se použije z tabulky. Ale aproximace nebude příliš blizka, v materiálech byste meli mít i způsob kontroly, zda je to dobrá aproximace. Ale pro rychlou kontrolu stačí zkontrolovat i graficky, co vychází)
OK?
EDIT: ještě jsem chtěla zkontrolovat, zda v úplně 1. tabulce - 1. příspěvek od ↑ kotry: jsou dvě ruzné hodnoty funkce pro x=0? Je to podivne - měla by byt jen jedna.
Offline
#15 02. 07. 2009 14:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Metoda nejmenších čtverců
↑ kotry:
Já netuším, který princip bys měl vysvětlovat - popis metody a vzorce najdeš v materiálech studujních i ve "stolních knihách techníků" - Rektorys, Bartsch, Strojirenské tabulky.
Pokud jde o teorii - tak stačí nastudovat zde,včetně odkazů a případně se zeptej konkrétně, co je potřeba dovysvětlit.
Pokud o konkrétní zadání - tak opět, co konkrétně máme paní učitelce vysvětlovat.
Teď tu nebudu, ale do večerních hodin určitě budu, nebo někdo z odborně zdatnějších kolegů se toho ujme, děkuji :-)
Offline
#16 04. 07. 2009 12:12
Re: Metoda nejmenších čtverců
no ono šlo spíš o to, že počítání těmi vzorci (je sice jednoduší) je spíš matematická analýza-tento postup s námi neprobírala. Šlo jí jen o postup kterým jsme sestavili ty rovnice. Tím postupem co nám to vysvětlovala na přednáškách sice vyjdou ty samé rovnice v matici, ale je to daleko pracnější a méně srozumitelné. Nakonec to stejně přešla a ani body v písemce nestrhávala :-)
takže paráda!
ještě jednou děkuji ;-)
Offline
#17 03. 02. 2010 19:16 — Editoval Kondr (03. 02. 2010 19:17)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Metoda nejmenších čtverců
Ze cvičných důvodů bych přihodil postup, jak to řešit pomocí přeurčené soustavy rovnic. Budeme chtít aby platilo f(x)=ax^2+bx+c. Tuto rovnost požadujeme v šesti bodech, což nám dává soustavu šesti rovnic pro neznáme a,b,c, tu zapíšeme maticí:
4 -2 1 |-10.7
1 -1 1|-6.7
0 0 1|-2.6
1 1 1|-2
4 2 1|-2.9
9 3 1|-6.1
Tato soustava pochopitelně nemá řešení, ale my se pokusíme nalézt alespoň "řešení". Vektor x=(a,b,c) získáme (viz Wiki) jako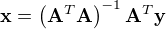
(Ověřeno Mathematicou, že vyjde stejně. S W|A si v tomto nerozumím.)
Důkaz ekvivalentnosti obou metod by jistě šlo podat z definice násobení matic.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#18 03. 12. 2010 16:19 — Editoval derek (04. 12. 2010 13:57)
Re: Metoda nejmenších čtverců
↑ Kondr:
Mohu se zeptat, jak jste to vypočetl? Úspěšně počítám touto metodou koeficienty pro křivku 1. stupňe. U 2. stupně mi vychází toto:
Dosazeny výše uvedené body podle wikipedie:
Matice  :
:
1.0 -2.0 4.0
1.0 -1.0 1.0
1.0 0.0 0.0
1.0 1.0 1.0
1.0 2.0 4.0
1.0 3.0 9.0
Matice 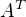 :
:
1.0 1.0 1.0 1.0 1.0 1.0
-2.0 -1.0 0.0 1.0 2.0 3.0
4.0 1.0 0.0 1.0 4.0 9.0
Matice 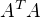 :
:
6.0 3.0 19.0
3.0 19.0 27.0
19.0 27.0 115.0
Matice 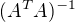 :
:
0.7640520134228188 0.8798238255033557 0.32424496644295303
1.3376677852348993 1.3680788590604027 1.3527684563758389
-0.13443791946308725 -0.0050335570469798654 0.020134228187919462
Matice  :
:
0.30138422818791955 0.20847315436241615 0.7640520134228188 1.9681208053691275 3.8206795302013425 6.321728187919463
4.0125838926174495 1.3223573825503354 1.3376677852348993 4.058515100671141 9.484899328859061 17.616820469798657
-0.043833892617449674 -0.10927013422818793 -0.13443791946308725 -0.11933724832214765 -0.06396812080536912 0.0316694630872483 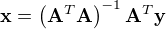 :
:
-60.2 -198.4 1.78
tedy dosazením zpět dle wiki: 
EDIT: problém vyřešen, měl jsem špatně naprogramovanou inverzi matice :)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Metoda nejmenších čtverců (TOTO TÉMA JE VYŘEŠENÉ)

