Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 06. 2024 13:38 — Editoval <h1>dydy</h1> (12. 06. 2024 13:40)
- <h1>dydy</h1>
- Příspěvky: 161
- Reputace: 0
Mohou být hlavní body H',H prohozené
Mohou být v optické soustavě hlavní(principal) body H,H' prohozené?Vždy je zleva doprava H a po něm H'. Ze symetrie na příapdech 1 a 5 na obrázku vyplývá taky, že tam hraje koli znaménková konvence a při zdrcadlení by bez toho by pořadí najednou bylo H' vlevo a H vpravo, což ovšem je odlišná optická soustava, ale ona je ve skutečnost stejná po zrcadlení, když je symetrická a to by byl spor.
Lepší tedy je mluvit o nějaké vzdálenosti těchto bodů se znaménkem, Například u soustavy tvořené jednou tenkou čočkou je ta vzdálenost nula.
Existuje nějaká optická soustava, kde tedy vzdálenost mezi H a H' nebude kladná ? A nebo to možné není? Čili že ty hlavní body vždy budou u svých vrcholů čoček ?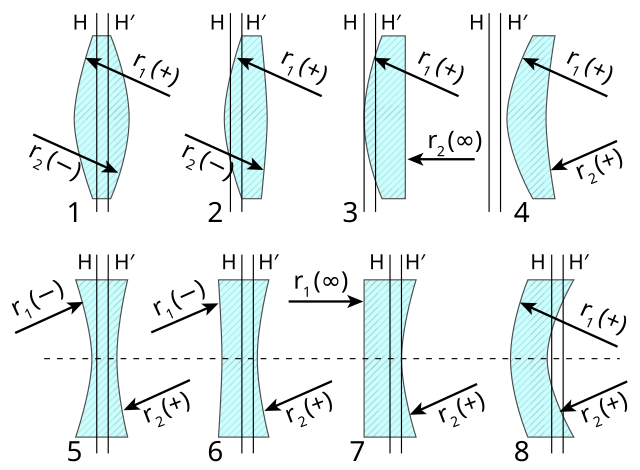
Offline
#2 13. 06. 2024 08:49
Re: Mohou být hlavní body H',H prohozené
Osobně si myslím, že ani žádná fyzická jedna čočka ani jejich kombinace nemůže vytvořit něco, co je kratší než ideální čočka, tj. aby ta tvá vzdálenost vyšla záporná. Ale úplně s jistotou to samozřejmě nevím.
Offline
#3 22. 06. 2024 18:24
- Mirek2
- Příspěvky: 1195
Re: Mohou být hlavní body H',H prohozené
Obrazem bodu H je bod H' - a naopak.
Kde je na obrázku H a H' souvisí s tím, kde je předmětový a obrazový prostor.
Pro tenkou čočku je myslím z definice [mathjax]d\ll r_2-r_1[/mathjax], pak [mathjax]HH'\approx d(n-1)/n[/mathjax].
Ohledně znamének se zkus podívat třeba sem (nevím):
https://muj.optol.cz/chlup/fuka_havelka/
Offline
#4 23. 06. 2024 10:32
Re: Mohou být hlavní body H',H prohozené
Otázka je podobná tomu, jestli fyzická vzdálenost ohnisek může být menší než dvojnásobek ohniskové vzdálenosti.
Nemusel by být zas tak velký problém to dokázat. Zdá se celkem logické že v “inverzní optice” kde jsou čočky z opticky řidšího materiálu než okolní prostředí by to tak mohlo být.
Offline
