Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 06. 08. 2009 18:43 — Editoval lukaszh (06. 08. 2009 19:51)
Re: Goniometrická rovnice
↑ Sirrek:
Malý hint: Umocni obe strany. Využi rovnosti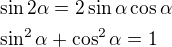
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#6 06. 08. 2009 19:22 — Editoval BrozekP (06. 08. 2009 19:39)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Goniometrická rovnice
↑ lukaszh:
Tvé řešení není dobře, použil jsi neekvivalentní úpravu. Je třeba provést zkoušku a vyloučit tak x, která rovnici neřeší. Jiná možnost než provádět zkoušku je např. všimnout si, že pravá strana před umocněním je vždy nezáporná. Pokud budeme uvažovat pouze taková x, pro která je i levá strana nezáporná (tj. ![kopírovat do textarea $x\in\bigcup_{k\in\mathbb{Z}}\[-\frac{\pi}4+2k\pi,\,\frac34\pi+2k\pi\]$](/mathtex/9a/9a514665b76465cd4d95a5fc870f879c.gif) ), bude umocnění ekvivalentní úprava.
), bude umocnění ekvivalentní úprava.
A pak také není dobře úprava
,
vypadla ti dvojka.
Offline
#7 06. 08. 2009 19:53
Re: Goniometrická rovnice
↑ BrozekP:
Vedel som, že umocnenie je neekvivalentná operácia, ale že to až takto s tým preženiem :-( ... Bolo to v rýchlosti. Zopakujem si základy ;-) Na skúšky som nikdy nemal čas a teraz mi chýbajú...
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#9 06. 08. 2009 20:38 — Editoval BrozekP (06. 08. 2009 20:39)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Goniometrická rovnice
↑ Sirrek:
Který krok není v ↑ postupu od lukaszhe: jasný? (Postup tam je skrytý, musíš kliknout na odkaz Zobrazit.)
Offline
#13 06. 08. 2009 21:19
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Goniometrická rovnice
↑ B4r:Celkem častá chyba je dělit rovnici něčím, co může být 0, zde sin(x). Proto je lepší vytknout než dělit. Řešení jsou i všechna čísla tvaru 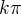 .
.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#19 06. 08. 2009 23:39
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Goniometrická rovnice
↑ Sirrek:Položme sin(u)=s, cos(u)=c. Daná rovnice
s/c+c/s=8sc, po vynásobení sc
ss+cc=8sscc, ale goniometrická jednička říká ss+cc=1 (dosadíme nalevo), navíc 2sc=sin(2u) (dosadíme napravo), takže
1=2sin^(2u). Dál už je to trivialita.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#21 07. 08. 2009 09:34
Re: Goniometrická rovnice
↑ Sirrek: Ještě k té první rovnici a návrhu řešení přes neekvivalentní úpravu umocněním ↑ lukaszh: a pak analýzou výsledku ↑ BrozekP:.
Jde se na to podívat také ekvivalentně takto: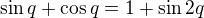
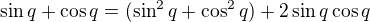
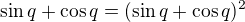
No a zřejmě 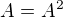 je pouze pro
je pouze pro  a
a  , kde
, kde 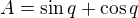 .
.
Offline
.png)

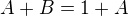
.png)
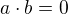 ak a je nula, alebo b je nula, prípadne a aj b sú sučasne nuly. Riešiť treba teda dve rovnice
ak a je nula, alebo b je nula, prípadne a aj b sú sučasne nuly. Riešiť treba teda dve rovnice
.png)
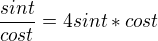
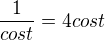
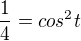
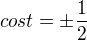
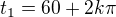
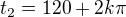
.png)
.png)