Matematické Fórum

musixx · 07. 01. 2009 15:10

Zdravim vas, kolegove, a preji hodne vypsanych tuzek (pri pocitani, samozrejme) do noveho roku!

Pres Vanoce jsem se trapil s touto ulohou, zatim ji nemam udelanu. Potrebuji to analyticky vypocitat, ale samozrejme jakekoli popostrceni by mi stacilo. Konkretni vypocty si udelam sam, jde mi spis o ideu, jak na to jit. Jsme v klasickem 3D prostoru, znaceni standardni.

I. Trojuhelnik ABC, zname delky jeho stran.

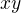II. Tri vzajemne ruzne roviny $\sigma_i$ , ( $i=1,2,3$ ), vsechny kolme na $xy$ a vsechny obsahuji pocatek souradneho systemu.

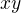III. V kazde rovine $\sigma_i$ mame kruznici $k_i$ s polomerem $r_i$ . Pro zacatek muzeme uvazovat zjednoduseni: stredy kruznic v rovine $xy$ . Stredy kruznic samozrejme take zname.

IV. Vime, ze trojuhelnik ABC lze umistit tak, ze 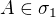$A\in\sigma_1$ , $B\in\sigma_2$ , $C\in\sigma_3$ . Alespon jedno reseni existuje, to vime (trojuhlenik ma takove delky stran a stredy kruznic jsou umisteny tak, ze to jde).

Jak vypocitat polohy bodu A,B,C (jiz umisteneho trojuhelnika podle bodu IV)?

Diky za rady, napady, pripominky.

musixx · 10. 08. 2009 13:52 — Editoval musixx (10. 08. 2009 13:56)

Vidím, že přes prázdniny je tady tak trochu mrtvěji, tak jsem si vzpomněl na jeden svůj starší problém. Kdyby se třeba někomu chtělo...

Možná to původní zadání je až zbytečně komplikované. Je o to umístit trojúhelník známých rozměrů tak, aby každý jeho vrchol ležel na jedné ze tří kružnic v prostoru. Kružnice mají známé (nestejné) poloměry.

Možná zjednodušení:

1. kružnice leží v rovinách kolmých na xy
2. kružnice mají středy v xy
3. 1+2+roviny kružnic svírají mezi sebou 120°

Byl bych rád i za nápad jak na to při zjednodušeních.

Kondr · 10. 08. 2009 14:36

Body A,B,C mají celkem 9 souřadnic, tedy 9 neznámých. Z toho, že leží na kružnicích vyplývá 6 rovnic, z toho, že známe strany trojúhelníku další tři. Jde celkem o soustavu 6 kvadratických a 3 lineárních rovnic o 9 neznámých. Zkoušel jsi ji řešit?

Pavel Brožek · 10. 08. 2009 14:48

Obecně tedy máš středy kružnic $S_i[m_i,\,n_i,\,o_i]$ , kružnice mají poloměry $r_i$ , leží v rovině, která má normálový vektor $(\alpha_i,\,\beta_i,\,\gamma_i)$ , vrcholy trojúhelníku označíme $[x_i,\,y_i,\,z_i]$ a trojúhelník má strany $a,\,b,\,c$ . Máme teda soustavu devíti rovnic o devíti neznámých, o které víme, že má řešení.

$(x_1-m_1)^2+(y_1-n_1)^2+(z_1-o_1)^2=r_1^2\nl (x_2-m_2)^2+(y_2-n_2)^2+(z_2-o_2)^2=r_2^2\nl (x_3-m_3)^2+(y_3-n_3)^2+(z_3-o_3)^2=r_3^2\nl \alpha_1(x_1-m_1)+\beta_1(y_1-n_1)+\gamma_1(z_1-o_1)=0\nl \alpha_2(x_2-m_2)+\beta_2(y_2-n_2)+\gamma_2(z_2-o_2)=0\nl \alpha_3(x_3-m_3)+\beta_3(y_3-n_3)+\gamma_3(z_3-o_3)=0\nl (x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2=a^2\nl (x_2-x_3)^2+(y_2-y_3)^2+(z_2-z_3)^2=b^2\nl (x_3-x_1)^2+(y_3-y_1)^2+(z_3-z_1)^2=c^2\nl$

Vidím, že už Kondr odpověděl, tak jsem ji alespoň vypsal :-)

musixx · 10. 08. 2009 14:57 — Editoval musixx (10. 08. 2009 15:31)

↑ Kondr: ↑ BrozekP: Zdravím vás oba a díky za tip.

Tímto směrem jsem na to ještě nešel (s normálami rovin coby vstupem) a vypadá to minimálně hezky symetricky říct, že body leží na koulích a pak to doupřesnit na patřičné kružnice pomocí skalárního součinu.

Moje pokusy se zatím spíš držely toho, že jsem se snažil vrcholy trojúhelníka hledat na kružnicích ve tvaru 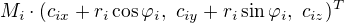$M_i\cdot(c_{ix}+r_i\cos\varphi_i,\ c_{iy}+r_i\sin\varphi_i,\ c_{iz})^T$ se známými maticemi $M_i$ , čímž jsem měl jen tři neznámé, jenže zase jako argumenty goniometrických funkcí.

Je to ale už nějaká doba. V příštích dnech mrknu na váš tip a případně dám vědět. Zatím díky!

Matematické Fórum

#1 07. 01. 2009 15:10

Zajimava stereometricka uloha

#2 10. 08. 2009 13:52 — Editoval musixx (10. 08. 2009 13:56)

Re: Zajimava stereometricka uloha

#3 10. 08. 2009 14:36

Re: Zajimava stereometricka uloha

#4 10. 08. 2009 14:48

Re: Zajimava stereometricka uloha

#5 10. 08. 2009 14:57 — Editoval musixx (10. 08. 2009 15:31)

Re: Zajimava stereometricka uloha

Zápatí