Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Objem tělesa vázaný podmínkou (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 08. 2009 16:30
Objem tělesa vázaný podmínkou
Nechť  a
a  jsou dvě nezáporná čísla vázaná podmínkou
jsou dvě nezáporná čísla vázaná podmínkou 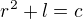 , kde
, kde  je napřed dané kladné číslo. Definujme funkci
je napřed dané kladné číslo. Definujme funkci
Najděte hodnoty čísel  a
a  (závislých na
(závislých na  ) tak, aby objem
) tak, aby objem  tělesa, které vznikne rotací plochy omezené křivkou
tělesa, které vznikne rotací plochy omezené křivkou  ,
, 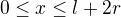 , a osou x kolém osy x, byl maximální.
, a osou x kolém osy x, byl maximální.
Offline
#2 12. 08. 2009 19:00
Offline
#3 12. 08. 2009 19:35
Re: Objem tělesa vázaný podmínkou
↑ jarrro:
Není to správně. Je tam chyták.
Pokud si nebudeš vědět rady, otevři nápovědu k odhalení chyby.
Offline
#4 12. 08. 2009 19:55
Re: Objem tělesa vázaný podmínkou
MATH IS THE BEST!!!
Offline
#6 13. 08. 2009 10:56 — Editoval BrozekP (13. 08. 2009 11:08)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Objem tělesa vázaný podmínkou
Offline
#7 13. 08. 2009 11:18 — Editoval jarrro (13. 08. 2009 11:22)
Re: Objem tělesa vázaný podmínkou
MATH IS THE BEST!!!
Offline
#8 13. 08. 2009 11:47
Re: Objem tělesa vázaný podmínkou
Offline
#9 13. 08. 2009 11:55 — Editoval BrozekP (13. 08. 2009 11:56)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Objem tělesa vázaný podmínkou
Offline
#10 13. 08. 2009 11:59
Re: Objem tělesa vázaný podmínkou
↑ BrozekP:
Bravo! Tedy musí být
Úlohu jsem zařadil zde proto, že jsem tušil odbočení ze správné cestičky řešení. Je třeba si uvědomit, že i u standardně znějících úloh musíme brát na zřetel všechny parametry úlohy - situace z praxe jako vystřižená.
Offline
#11 13. 08. 2009 13:34 — Editoval jarrro (13. 08. 2009 13:36)
Re: Objem tělesa vázaný podmínkou
MATH IS THE BEST!!!
Offline
#13 14. 08. 2009 15:39 — Editoval Rumburak (14. 08. 2009 15:53)
Re: Objem tělesa vázaný podmínkou
↑ Marian:, ↑ jarrro:, ↑ BrozekP:
Zdravím vás, kolegové.
Dopracoval jsem se k mezivýsledku
a za Boha se mi nedaří objevit, jakým trikem lze maximum této funkce nalézt "hezky".
Pochopil bych to, kdybychom místo funkce f vzali funkci
Offline
#14 14. 08. 2009 16:29
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Objem tělesa vázaný podmínkou
Offline
#15 14. 08. 2009 16:46
Re: Objem tělesa vázaný podmínkou
↑ BrozekP:
Marian píše:
"Vyjde to velice hezky. Musel jsem se chvíli ujišťovat při analýze úlohy. Je to snažší, než si myslíš. Vlastně není potřeba ani papír."
Čekal jsem proto, že se nabízí nějaký chytrý trik, kdy nebude nutno vyšetřovat průběh funkce běžnými prostředky,
při čemž se nějaký ten "list papíru" obvykle spotřebuje, pokud vyšetřovaná funkce není dostatečně jednoduchá.
Ale nevadí, až budu mít více souvislého volného času, pustím se do toho.
Zatím děkuji za reakci.
Offline
#16 14. 08. 2009 17:03
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Objem tělesa vázaný podmínkou
↑ Rumburak:
Myslím, že se Marian vyjadřoval už pouze k dořešení úlohy pro c<1. S tím, že už máš na papíře úlohu vyřešenou pro c≥1, to jde z hlavy.
Offline
#17 20. 08. 2009 21:07
Re: Objem tělesa vázaný podmínkou
↑ BrozekP:
Ano, skutečně jsem se vyjadřoval pouze k případu, který zmiňuje BrozekP. Děkuji mu za doplnění.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Objem tělesa vázaný podmínkou (TOTO TÉMA JE VYŘEŠENÉ)
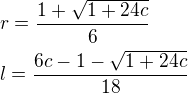
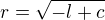 pre
pre ![kopírovat do textarea $c\leq\frac{3}{\sqrt[3]{50}}$](/mathtex/1d/1da03a2eba3660dd5d5f18a9def38fea.gif) pre
pre ![kopírovat do textarea $c\in \left(\frac{3}{\sqrt[3]{50}};1\right)$](/mathtex/a3/a3c68168e5822f6b64b8680987120d3c.gif) ma zatiaľ nič nenapadá pre väčšie ako jedna som už písal vyššie
ma zatiaľ nič nenapadá pre väčšie ako jedna som už písal vyššie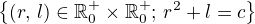 , globální maximum proto bude na hranici této množiny.
, globální maximum proto bude na hranici této množiny. .
.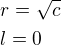 ?
?![kopírovat do textarea $r \in [0,\,\sqrt c]$](/mathtex/19/19a15f57d74d3decd0172afa20fb2dd1.gif) :
: 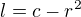 a
a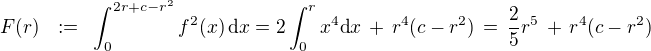
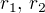 splňující
splňující 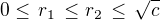 a jim (a funkci g) přiřazená rotační tělesa
a jim (a funkci g) přiřazená rotační tělesa 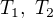 platí
platí 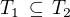 .
.