Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Prirodzený logaritmus (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 08. 2009 20:12
Prirodzený logaritmus
Ahojte,
dnes sa mi podarilo odvodiť jeden, aspoň pre mňa zaujímavý vzťah. Nikde som sa s ním doposiaľ nestretol. Je to 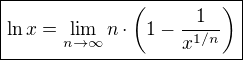
Počítajme integrál s neznalosťou 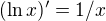

Zvolím malé číslo omega, pričom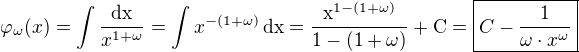
Omegu definujem ako zlomok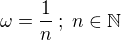
Potom výsledok vyzerá nasledovne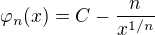
Viem, že limitne 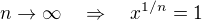 , teda daná funkčná postupnosť nekonverguje k žiadnej "normálnej funkcií. Prirodzene sa mi núka voliť
, teda daná funkčná postupnosť nekonverguje k žiadnej "normálnej funkcií. Prirodzene sa mi núka voliť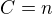
pričom potom možno uvažovať o konvergencii ako takej. 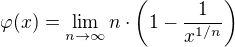
Všetci určite vieme, že funkcia  je prirodzený logaritmus, no robím sa, že neviem. Je to nejaká neznáma funkcia. Ako by sa dalo z tohto zápisu prísť na to, že ide o prirodzený logaritmus? Alebo aspoň zistiť, že funkcia sa správa ako každá iná logaritmická funkcia? Overme napríklad
je prirodzený logaritmus, no robím sa, že neviem. Je to nejaká neznáma funkcia. Ako by sa dalo z tohto zápisu prísť na to, že ide o prirodzený logaritmus? Alebo aspoň zistiť, že funkcia sa správa ako každá iná logaritmická funkcia? Overme napríklad 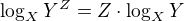
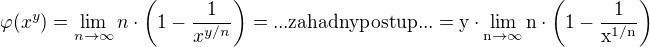
Záhadný postup je záhadný postup. Neviem, akým spôsobom sa dá na toto prísť. O logaritme nenapovie veľa ani určitý integrál, ktorý nevyužíva záhadné konštanty :-)![kopírovat do textarea $\int_{A}^{B}\frac{\rm{d}x}{x^{1+\omega}}=\int_{A}^{B}x^{-(1+\omega)}\,\rm{d}x=\left[-\frac{1}{\omega\cdot x^{\omega}}\right]_{A}^{B}=\frac{1}{\omega\cdot A^{\omega}}-\frac{1}{\omega\cdot B^{\omega}}=\frac{n}{A^{1/n}}-\frac{n}{B^{1/n}}$](/mathtex/3e/3e32b5db82b3862532437d398f9354ab.gif)
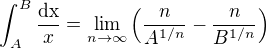
Vďaka za tipy.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#2 23. 08. 2009 22:03 — Editoval BrozekP (23. 08. 2009 22:04)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prirodzený logaritmus
lukaszh napsal(a):
Ako by sa dalo z tohto zápisu prísť na to, že ide o prirodzený logaritmus?
Já bych tu limitu prostě spočítal. Ale nejsem si jistý, jestli je to to, o co ti jde.
Offline
#3 23. 08. 2009 22:34
Re: Prirodzený logaritmus
Pokud bych mohl zaměnit limitu posloupnosti za limitu funkce (což doufám, že v tomto případě možné je), dostal bych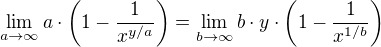
substitucí 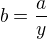 .
.
Ještě co mě teď k tomu napadlo, je že ten vztah nápadně připomíná cosi "inversního" ke známému vztahu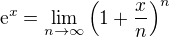
Nechť totiž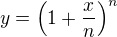
k tomu je inversní funkce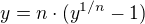 .
.
Nějakým limitním přechodem, který teď večer už určitě dohromady nedám (ovšem neručím, že během dne ano), bychom snad mohli dostat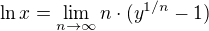
odkud už by se vztah nalezený kolegou lukaszem dostal analogií se vztahem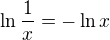 .
.
Dobrou noc.
Offline
#4 24. 08. 2009 08:01
Re: Prirodzený logaritmus
↑ Olin:
Cez ten inverz to vidím zatiaľ ako jedinú schodnú cestu. Vďaka za tip. Potom by to bolo
Teraz budem pracovať už len s inverznou ![kopírovat do textarea $y_n=n\cdot\(\sqrt[n]{x}-1\)=\sqrt[n]{x}\cdot n\cdot\(1-\frac{1}{\sqrt[n]{x}}\)$](/mathtex/60/60794c3dec0cfc992398e394ff67f075.gif)
Teraz za predpokladu, že existuje konečná limita postupnosti ![kopírovat do textarea $a_n=n\cdot\(1-\frac{1}{\sqrt[n]{x}}\)$](/mathtex/2a/2ae769b29ba9224e77f1339ed2798394.gif) , tak možno použiť vetu o súčine
, tak možno použiť vetu o súčine ![kopírovat do textarea $\lim_{n\to\infty}\sqrt[n]{x}\cdot a_n=1\cdot\lim_{n\to\infty}a_n$](/mathtex/df/df0b319b0e28b81a82e0f5a00a7afc34.gif)
a je to :-) Všade predpokl. že  .
.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#5 24. 08. 2009 10:12 — Editoval BrozekP (24. 08. 2009 10:13)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prirodzený logaritmus
lukaszh napsal(a):
Všetci určite vieme, že funkcia
je prirodzený logaritmus.
A to víme jak? Kdybys zvolil 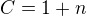 , tak by to třeba nebyl přirozený logaritmus. To, že je to přirozený logaritmus, bych určil z výpočtu té limity
, tak by to třeba nebyl přirozený logaritmus. To, že je to přirozený logaritmus, bych určil z výpočtu té limity
Offline
#6 24. 08. 2009 12:12
Re: Prirodzený logaritmus
↑ lukaszh:
Osobně jsem s tímto přístupem již setkal. Doporučuji se informovat ve skriptech prof. Müllera z university v Trieru (GER), Věta 5.14 na stránce 41 v kapitole Posloupnosti (=Folgen). Úvaha pokračuje až na stránku 44.
Je tam de facto prezentován jistý korektní přístup zavedení logaritmické funkce, který se nevidí v českých učebnicích. Pro inspiraci výše zmíněného stahujte PDF verzi volně z autorových stránek zde.
Offline
#7 24. 08. 2009 12:23
Re: Prirodzený logaritmus
↑ BrozekP:
Vďaka za výpočet. Zistil som, že bez samotného výpočtu, ťažko odvodzovať nejaké vlastnosti logaritmu.
↑ Marian:
Určite si to prečítam, vďaka.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Prirodzený logaritmus (TOTO TÉMA JE VYŘEŠENÉ)
