Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 08. 2009 16:45
Re: Integrál
Offline
#3 24. 08. 2009 16:58
Re: Integrál
Offline

 a
a ![kopírovat do textarea $g:\quad [0,1]\maps\mathbb{R}$](/mathtex/b3/b34d0565856b897e138c74ece818937c.gif) . Jestliže
. Jestliže  , pak platí
, pak platí
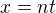 snadno nahlédneme, že
snadno nahlédneme, že  .
.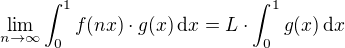 ,
, 
 , takže pro libovolné
, takže pro libovolné  je
je 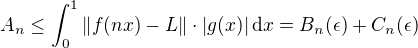 , kde
, kde  ,
, 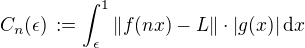 .
.  ,
,  , kde supremum uvažujeme vždy vzhledem k definičnímu oboru příslušné funkce.
, kde supremum uvažujeme vždy vzhledem k definičnímu oboru příslušné funkce.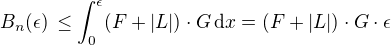 . Důležité je, že tento odhad je stejnoměrný vzhledem k n.
. Důležité je, že tento odhad je stejnoměrný vzhledem k n. je pevně zvoleno ve výše uvedeném rozsahu. Z předpokladu o limitě funkce f v nekonečnu plyne existence konstanty
je pevně zvoleno ve výše uvedeném rozsahu. Z předpokladu o limitě funkce f v nekonečnu plyne existence konstanty  takové, že
takové, že 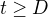 je
je  . Položme nyní
. Položme nyní  .
. a
a 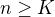 je tedy
je tedy 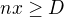 , takže potom
, takže potom 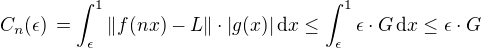 .
. , čímž je věta dokázána.
, čímž je věta dokázána.