Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 24. 08. 2009 23:52
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Dva technické vztahy
↑ Zbyšek:
Zdravím,
(nejsem si úplně jista se zadáním, ale předpokládám, že F_1, 1 je dolní index, a v dalším zadání také dolní indexy, je to tak?) levou a pravou stranu logaritmuji (dekadickým log):
levou a pravou stranu logaritmuji (dekadickým log):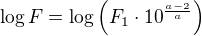 podle pravidel počítání s logaritmy dostanu:
podle pravidel počítání s logaritmy dostanu: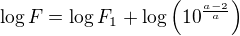

od tohoto kroku už zvladneš?
---------------------------------------------------------- osamostatnuji vyraz s ln:
osamostatnuji vyraz s ln: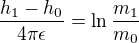 podle pravidel pocitani s logaritmy:
podle pravidel pocitani s logaritmy: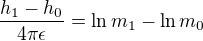 dál už se podaří?
dál už se podaří?
Případně se ozví, co se podařilo.
Offline


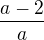 exponent čísla 10 nějak mi blbne TeX v návrhu se zobrazuje dobře ale po odeslání se to zobrazí jako a-2a
exponent čísla 10 nějak mi blbne TeX v návrhu se zobrazuje dobře ale po odeslání se to zobrazí jako a-2a