#2 01. 09. 2009 17:06
Re: Převod DNF do KNF
z tehle formule vidis presne, pro ktere kombinace ohodnoceni x,y,z je formule pravdiva; jsou to presne ty uvedene v jednotlivych zavorkach
tedy formule je pravdiva kdyz x=0,y=0,z=0 nebo kdyz x=0,y=0,z=1 atd.
negace formule a & b je (not a) OR (not b) a naopak, tedy si staci vytvorit formuli F opacnou k te zadane ve stejnem tvaru (takovou formuli, ze je pravda kdyz puvodni ne, udelas proste disjunkci takovych kombinaci x,y,z pro ktere je puvodni formule 0) a F znegovat
Offline
#4 01. 09. 2009 17:32
Re: Převod DNF do KNF
Jo aha uz asi tusim, kdyz mam to x,y,z 0,0,0, tak mi vyjde 1 v ty prvni zavorce, protoze to jsou konjunkce a ty jsou dve jednicky rovny 1 a jelikoz to jsou negace, tak to je 1,1,1, v ty zavorce a tak dal, ale dal uz nejak nechapu co s tim, kdyz sem si zjistil, jaky ohodnoceni potrebuju aby byly pravdivy
Offline
#5 01. 09. 2009 17:40
Re: Převod DNF do KNF
No ted si zkonstruujes formuli v tomhle tvaru, ktera je presne opacna. Tedy vezmes vsechny ohodnoceni, pro ktere puvodni formule NENI pravdiva, a z nich si stejnym zpusobem postavis formuli. Tu pak klasickym zpusobem znegujes (vsechny disjunkce zmenis na konjunkce, vsechny konjuknce na disjunkce, a vsechny vyskyty x,y,z jen znegujes)
po krocich: tahle f je pravdiva pro 000 001 010 011 101. chces opacnou formuli, tedy takovou co je pravdiva pro 111,110,100; tzn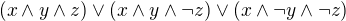 
. a tu znegujes -> 
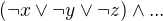mozna jsem udelal chybku tak si to radsi prekontroluj
Offline
#7 01. 09. 2009 18:09
Re: Převod DNF do KNF
na druhou stranu ten postup funguje presne opacne -- znegujes knf formuli, dostanes nejakou dnf, podivas se kdy je ta pravdiva a zkonstruujes dnf ktera je jeji negaci. Ale nevim jestli neexistuje nejaky hezci postup, tohle me jen ted napadlo (tim myslim pro oba smery)
Offline