Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 08. 2009 10:47
Kardinální a ordinální čísla
Mám v tom nejasnost :)
Ordinální čísla definujme jakkoliv, třeba jako typy dobře uspořádaných množin. Kardinální čísla budiž začátky těch ordinálních, eg. kardinální číslo budiž vždy nejmenší ordinál jisté mohutnosti.
Problém mám s tím, že pokud nemáme axiom výběru, nemáme zaručeno, že každou množinu lze dobře uspořádat. Pak ovšem pro množiny které nejdou dobře uspořádat, nemáme definovaná kardinální čísla, charakterizující jejich mohutnost... je to tak?
A pokud to tak je, tak dá se vůbec u těchto množin mluvit o jejich mohutnosti? Je možné, že bez AC existují dvě množiny A, B, pro které nelze rozhodnout, zda existuje injektivní fi: A->B nebo naopak? Nebo o tom vůbec nemá smysl mluvit?
Offline
#3 01. 09. 2009 18:03
Re: Kardinální a ordinální čísla
neni :). Kardinalni cislo je definovano pro vsechny mnoziny ktere jsou isomorfni nejakym ordinalum. A k tomu aby jsi umel najit isomorfismus na ordinal, musis umet prvky mnoziny seradit do transf. sekvence, tedy dobre usporadat. Predstav si mnoziny ve kterych je strasny bordel, ze at zkousis jakykoli usporadani, nikdy neudelas dobry (predstav si realna cisla). A porovnavani pres proste funkce ti taky moc nepomuze: mas dve osklive mnoziny, tak zkousis definovat proste funkce z jedne do druhe postupnym pribiranim prvku -- a bez AC nemas zaruceno, ze funkce kterou stavis je nejak omezena; muze se ti stat ze at zkousis jakkoli, porad bude neco zbyvat
Offline
#4 03. 09. 2009 10:37 — Editoval Rumburak (03. 09. 2009 11:02)
Re: Kardinální a ordinální čísla
S tvrzením
(T1) každou dobře uspořádanou množinu lze injektivně zobrazit na některé kardiníální číslo
asi není problém. Snadno nahlédneme, že platí též obrácené tvrzení
(T2) injektivní obraz kardinálního čísla je množina, kterou lze dobře uspořádat.
Důkaz: Nechť  je kardinální číslo,
je kardinální číslo,  injektivní (=prosté) zobrazení definované na množině
injektivní (=prosté) zobrazení definované na množině  ,
,  obraz množiny
obraz množiny 
při tomto zobrazení. Kardinální číslo je zároveň ordinálním číslem, tudíž je dobře uspořádáno relací 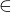 .
.
Na množině  definujme relaci
definujme relaci .
.
Snadno ověříme, že jde o dobré uspořádání množiny  .
.
Z uvedeného plyne, že tvrzení
(T3) každá množina je ekvivalentní některému kardinálnímu číslu
je ekvivalentní axiomu výběru.
Offline